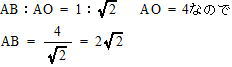高校受験はプロにお任せ/プロ家庭教師集団スペースＯＮＥの慶応女子高校2022年度数学入試問題座標平面

慶應義塾女子高校過去問傾向と対策
高校受験指導はプロ家庭教師集団スペースONEにお任せください。

慶応義塾女子高校過去問貝瀬悦

慶應義塾女子高等学校数学過去問研究

慶応義塾女子高校2022年度一般入学試験は2月10日に実施され募集人数約80名　志願者数455名　受験者数437名　合格者数127名　補欠発表数24名　補欠許可数0名　入学者63名でした。

数学入試問題は1.小問集合2問　2.平面図形　3.数の性質　4.座標平面　5.空間図形　が出題されました。慶應義塾女子高校の大問は、各問によって誘導されますので、手順を踏んで解きましょう。誘導に添う解法は慶應義塾女子校の過去入試問題を解くことによって身についていきます。

今回は　4.座標平面を解説します。

慶応義塾女子高校2022年度数学入試問題4.座標平面　問題

慶応義塾女子高校2022年度数学入試問題4.座標平面[1]解説解答

[1]　2点B，Dの座標及び定数aの値を求めなさい。

解説解答

慶應義塾女子高校過去問数学

三角形OABは線分OAを斜辺とする二等辺三角形なので、AOの中点をMとすると、△ABMはAM = BMの直角二等辺三角形となる。　

よって　AM = MO = AB = 2　　B(- 2，2)

慶応義塾女子高校2022年度数学入試問題4.座標平面[2]解説解答

[2]　点Cの座標を求めなさい。

解説解答

慶應義塾女子高校プロ家庭教師

慶応義塾女子高校2022年度数学入試問題4.座標平面[3]解説解答

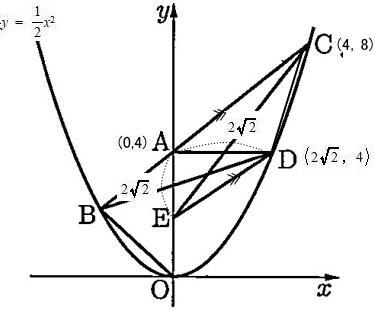
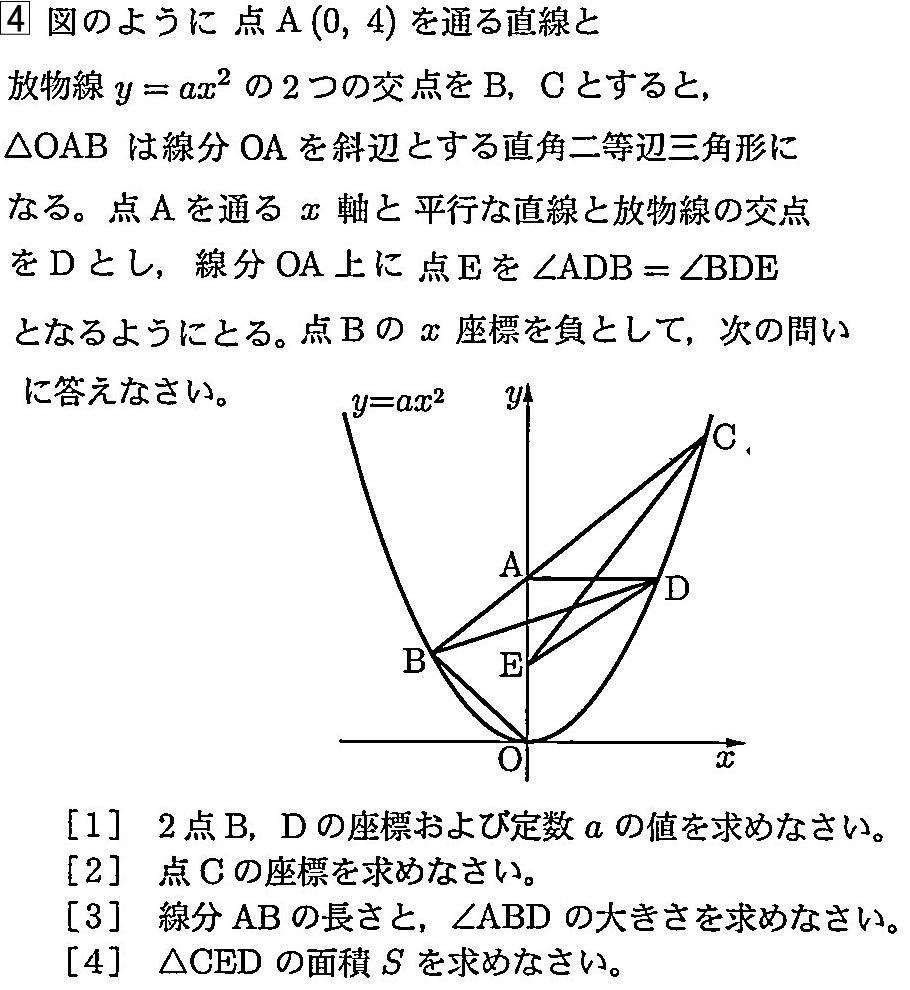
[3]　線分ABの長さと、∠ABDの大きさを求めなさい。

解説解答

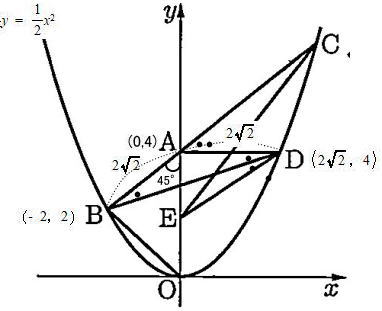
高校受験に次関数

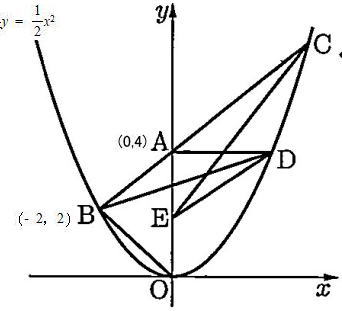
△OABは　AB = BOの直角二等辺三角形で、AO = 4なので　直角二等辺三角形の辺の比より

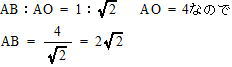
高校受験一次関数

△ABDは　AB = ADの二等辺三角形

よって　∠ABD = ∠BDA　三角形の1つの外角は、その隣にない2つの内角の和と等しいので

∠CAD = ∠ABD + ∠BDA = 2× ∠ABD

∠DAB = ∠DAE + ∠EAB = 90° + 45° = 135°

よって　2×∠ABD = 180° - 135° = 45°

したがって　∠ABD = 45° ÷ 2 = 22.5°

慶応義塾女子高校2022年度数学入試問題4.座標平面[4]解説解答

[4]　△CEDの面積Sを求めなさい。

解説解答

慶應義塾女子高校過去問傾向と対策 高校受験指導はプロ家庭教師集団スペースONEにお任せください。