慶応義塾女子高校過去問貝瀬悦
慶應義塾女子高校過去問傾向と対策
高校受験指導はプロ家庭教師集団スペースONEにお任せください。
慶応義塾女子高校2023年度数学入試問題2.場合の数 問題
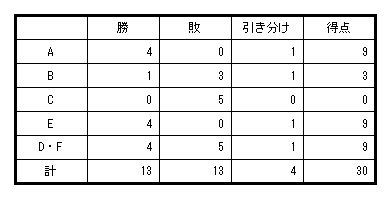
慶応義塾女子高校2023年度数学入試問題2.場合の数[1]解説解答
[1] 試合が1つ終わると、両チームに与えられる点の合計は何点か。
解説解答
勝ちチームに2点、負けチームに0点で合計2点
引き分けの場合それぞれにチームに1点 合計2点
したがって 両チームに与えられる点の合計は2点
答え 2点
解説解答
勝ちチームに2点、負けチームに0点で合計2点
引き分けの場合それぞれにチームに1点 合計2点
したがって 両チームに与えられる点の合計は2点
答え 2点
慶応義塾女子高校2022年度数学入試問題4.座標平面[2]解説解答
全6チームが試合を終えたとき、試合の総数は(あ)回になるから、Fチームの得点は(い)点である。AチームとEチームは得点が9点であるから、どちらも(う)勝(え)敗(お)引き分けである。したがって、Fチームは(か)勝(き)敗(く)引き分けしたことになる。
解説解答
総当たり戦は「全ての参加チームが、全ての相手と一定回数の対戦を行う方式」で、試合数は「対戦するチームの組み合わせの数×1試合」で求めることができる。
よって 6チームが他チームと1試合だけ対戦するので、対戦するチームの組み合わせは 6チームから2チーム選べばよいので
6×5÷(2×1) = 15通り
それぞれの対戦は1試合なので 15×1 = 15試合・・・(あ)答え
各試合で両チームに与えられる得点は2点なので、総得点数は 2×15 = 30点
よって Fチームの得点は 30 - (9 + 3 + 4 + 9) = 5点・・・(い)答え
1チームが他のチーム全試合に勝った場合の得点は 2×5 = 10点。4試合勝って1試合負けると得点は8点。4試合勝って1試合引き分けだと2×4+ 1 = 9点
AチームとEチームは得点が9点であるから、どちらも4勝0敗1引き分けである。・・・(う・え・お)答え
Bチームは得点が3点であり、Cチームには勝っているので1勝3敗1引き分け。
Cチームは得点が0点なので 0勝5敗0引き分け
A・B・C・Eの勝敗引き分け合計は9勝8敗3引き分け。
DチームとFチームの得点の合計は4 + 5 = 9点 よって2チームの勝敗は4勝5敗1引き分け。
Dチームは得点が4点でCチームには勝っているので、2勝3敗0引き分け または1勝2敗2引き分け
Fチームは得点が5点なので、2勝2敗1引き分け または1勝1敗3引き分け。
引き分け数の合計は4なので、当てはまるのはDチーム2勝3敗、Fチーム2勝2敗1引き分け・・・(か・き・く)答え
答え あ 15，い 5，う 4，え 0，お 1，か 2，き 2，く 1
慶応義塾女子高校2022年度数学入試問題4.座標平面[3]解説解答
[3] BチームとDチームのの負け試合数が同数のとき、Bチームが引き分けた試合の相手チームを答えなさい。
解説解答
Bチーム1勝3敗1引き分けと負け数が同数なのでDチームは2勝3敗0引き分け。
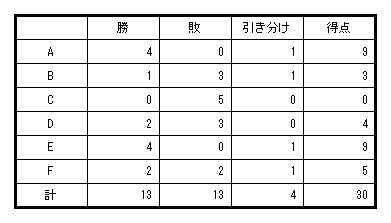
Bチームが引き分ける相手チームはA，E，Fのいずれか。
AチームとEチームもともに勝ち数が4なので、A・Eチームが引き分けの場合のみ、AチームはBCDFに勝ち、EチームもBCDFに勝つことができる。
したがって AチームとEチームが引き分けの場合、Bチームの引き分けの相手チームはF
答え Fチーム
