筑波大学附属高校過去問対策
2009年度筑波大学付属高等学校数学入試問題は 例年通り大問４題構成。１．小問集合６問 2．周上の点の移動 ３．平面図形 ４．空間図形 でした。
今回は 筑波大学付属高校入試頻出の ３．平面図形 を解説します。
筑波大学附属高校数学過去問対策
筑波大学附属高校過去問傾向と対策
国立大学付属高校受験はプロ家庭教師集団スペースONEにお任せください。
筑波大学附属高校2009年度 数学入試問題3.平面図形 問題
3. AB = AC = 13cm3cmの二等辺三角形ABCにおいて、辺BCの中点をMとする。
辺AB上に点D，辺AC上に点Eをとり、線分AMと線分DEの交点をFとしたところ AD = AF = 8cm，DF = 4cmであった。
このとき、次の⑩～⑫にあてはまる数を求めなさい。
(1) 線分AMの長さは (⑩)cmである。
(2) 線分DEの長さは(⑪)cmである。
(3) △DMEの面積は(⑫)c㎡である。
筑波大学附属高校2009年度 数学入試問題3.平面図形 (1) 解説解答
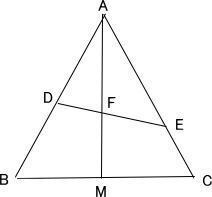
| (1) 線分AMの長さは(⑩)cmである。 |
| 解説 |
 |
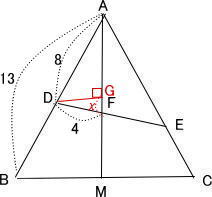| 点Dから辺AMに垂線を引き交点をGとする。 △ADGと△FDGともに直角三角形なので、ＧＦの長さをχとしすると、三平方の定理より 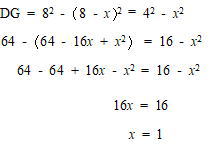 △ADG∞△ABMより 8：13 = (8 - 1)：AM  |
筑波大学附属高校2009年度 数学入試問題3.平面図形 (2) 解説解答
| (2) 線分ＤＥの長さは（⑪）ｃｍである。 |
| 解説 |
| 二種類の三角形の相似形を用いて考えます。 |
| 点ＥからＡＭに垂線を引き交点をＨとする。 |
 |
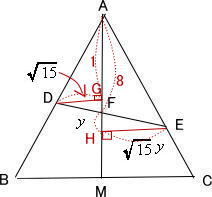| △DGＦ∞△ＥＨＦより 三平方の定理から |
 |
△ADG ∽ △AＨＥより |
 |
△DGＦ∞△ＥＨＦより |
筑波大学附属高校2009年度 数学入試問題3.平面図形(3) 解説解答
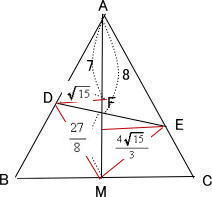
| (3) △DMEの面積は（⑫）ｃ㎡である。 |
| 解説 |
| |
 |
 |
 |
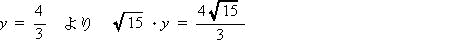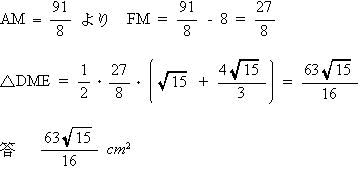