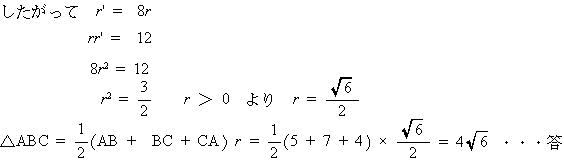筑波大学附駒場属高校過去問傾向と対策
国立大学付属高校受験はプロ家庭教師集団スペースONEにお任せください。

筑波大学附属駒場高校数学過去問対策

筑波大学付属駒場高等学校過去問研究

筑波大学附属駒場高等学校2014年度数学入試問題は、例年通り小問集合のない大問４題構成でした。

出題内容も例年通り　１．一次関数二次関数のグラフと図形（枝問３）　　２．数の性質（枝問３）　３．平面図形（枝問３）　４．空間図形（枝問3）でした。各大問とも　(1)(2)は解きやすい問題ですが、(3)は難問揃いです。応用レベルの問題を繰り返し学習し本番に備えましょう。

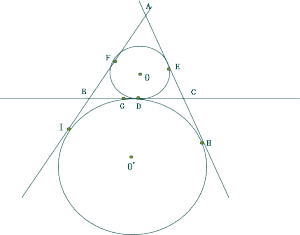
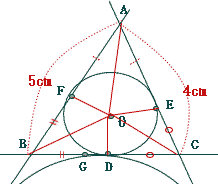
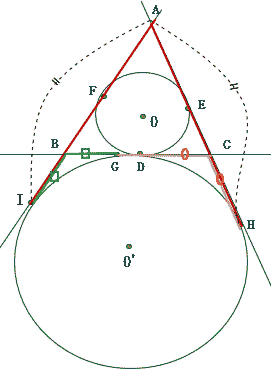
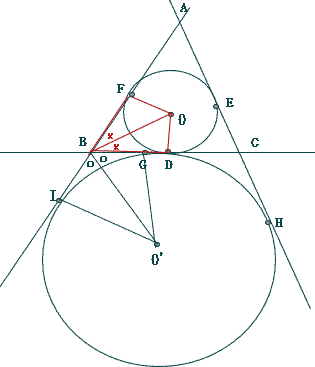
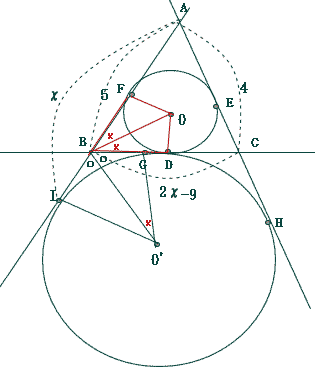
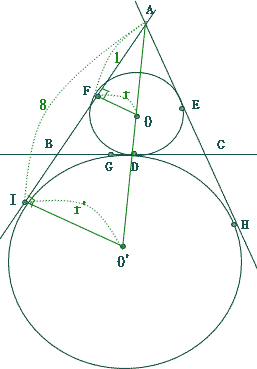
今回は　３．平面図形（枝問３）を解説します。補助線を使って求めていきましょう。

数学入試問題　３．平面図形


　　　　　　　　　　

筑波大学附属駒場高校2014年度数学入試問題3.平面図形　問題


3.　点Oを中心とする半径rcmの円Oと、点O'を中心とする変形r'cmの円O'があり、OO'＞(r + r')cmです。ただし、r＜r'とします。



図のように、２つの円O，O'に接する直線BC，CA，ABがあり、３点D，E，Fはこれらの直線と円Oの接点，３点G，H，Iはこれらの直線と円O'の接点です。また、AB = 5cm，CA = 4cmです。　AF + BD + CE = χcmとして、次の問いに答えなさい。

(1)　線分BC,AIの長さをそれぞれχの式で表しなさい。

(2) (ア) ∠OBO'の大きさを求めなさい。

　　(イ)rとr'の積rr'をχの式で表しなさい。(3)　rr' = 12 のとき、△ABCの面積を求めなさい。

筑波大学附属高校2009年度　数学入試問題3.平面図形　(1)　解説解答

(1)　線分BC,AIの長さをそれぞれχの式で表しなさい。

線分BCの長さ　解説解答　



円外の１点からその円に引いた２つの接線の長さは等しい。

（接線の対称性）から、AF = AE，BD = BF，CE = CD　

AF + BD + CE + AE + BF + CD = 2χ

また、AB = AF + BF = 5cm

AC = AE + CE = 4cm

AF + BD + CE + AE + BF + CD = 2χ

5 + 4 + BD + CD = 2χ

BD + CD = BC = 2χ- 9
　

線分AIの長さ　解説解答





円O'において、接線の対称性より　BI = BG，CH = CG，AI = AH

AI = AH = AB + BG + AC + CG = AB + AC + (BG + CG) = 5 + 4 + BC = 5 + 4 + 2χ- 9 = 2χ

AI + AH = 2AI = 2χ

したがって　

AI = χ


答　　BC = 2χ- 9，　　　AI = χ

筑波大学附属高校2009年度　数学入試問題3.平面図形　(2)　解説解答

(2) (ア) ∠OBO'の大きさを求めなさい。　　

解説解答



△OFBと△ODBにおいて、

OF = OD (半径)，FB = DB(接線の対称性)，BO = BO(共通)

対応する三辺がそれぞれ等しいので△OFB ≡ △ODB

従って　∠FBO = ∠DBO　・・・①

同様に　△O'GB ≡ △O'IB

従って　∠GBO' = ∠IBO'　・・・②


∠FBO + ∠DBO + ∠GBO' + ∠IBO' = 180°

(∠FBO + ∠IBO') + (∠DBO + ∠GBO') = 180°

①，②より

(∠FBO + ∠IBO') = (∠DBO + ∠GBO') なので

∠OBO'　= ∠DBO + ∠GBO' = 180÷2 = 90°

答　　　９０°


別解



円Oは△ABCの内接円なので、内心は三角形の3つの内角の二等分線の交点であることから、　

∠FBO = ∠DBO　・・・①

同様にBOは∠GBIの二等分線なので、∠GBO' = ∠IBO'　・・・②

①，②より

(∠FBO + ∠IBO') = (∠DBO + ∠GBO') なので

∠OBO'　= ∠DBO + ∠GBO' = 180÷2 = 90°

答　　　９０°


(イ)rとr'の積rr'をχの式で表しなさい。

解説解答



(ア)より　∠OBO'　= ∠DBO + ∠GBO' = 90°

よって　∠DBO = 90°- ∠GBO' ・・・①

また　△GBO'は　∠O'GB = 90°なので　∠BO'G = 90°- ∠GBO'　・・・②

①，②より　△ DBOと△GO'Bは直角と他の鋭角が等しいので　△ DBO ∽ △GO'B

よって　OD ：BG = DB ：GO' ・・・③


FB + DB = (AB + BC + CD) - ( AF + AE + EC + DC)

AF = AE ,　EC = DC なので　AF + AE + EC + DC = 2(AE + EC) = 2C より

FB + DB = AB + BC + CD - 2C = 5 + (2χ - 9) + 4 - 2×4 = 2χ - 8

FB = DB なので　DB = (2χ - 8)÷2 = χ - 4

OD = r ,　DG = r' ,　BG = IB = χ - 5 , DB = χ - 4 を③に代入して

r ： (χ - 5) = (χ　- 4) ：r'

内項の積 = 外項の積　より

r r' = (χ - 5)(χ　- 4) = χ2 - 9χ + 20 ・・・答




筑波大学附属高校2009年度　数学入試問題3.平面図形(3)　解説解答



(3)　rr' = 12 のとき、△ABCの面積を求めなさい。

解説解答



(2)(ア)より rr' = χ2 - 9χ + 20 = 12

χ2 - 9χ + 8 = 0

(χ- 8 )(χ- 1) = 0 　　χ = 1,8

2χ - 9＞ 0 なので　χ = 8

したがって　BC = 2χ - 9 = 2×8 - 9 = 7

BF = BD = χ- 4 = 8 - 4 = 4

AI = χ = 8

また　△AOFと△AO'Iにおいて

∠OFA = ∠O'IA = 90°

∠FAO = ∠IAO' (共通)　二角相等なので　△AOF ∽ △AO'I

OF：O'I = FA ：IA

OF = r ,O'I = r' なので

r：r' = (5-4)：8 = 1：8





Copyright(c) 2013 Sample Inc. All Rights Reserved. Design by http://f-tpl.com