高校受験はプロにお任せ/プロ家庭教師集団スペースＯＮＥの国学院久我山高校2025年度数学入試問題平面図形円の性質と相似形

國學院大學久我山高校数学入試問題解説解答
高校受験はプロ家庭教師集団スペースONEにお任せください。

国学院大学久我山高校過去問傾向と対策

國學院大學久我山高等学校過去問研究

國學院大學久我山高等学校の2025年度数学入試問題は　例年通り大問４題構成で、出題内容は１．小問集合10問　２．関数のグラフ　３．整数の性質　４．平面図形(円の性質と相似形)

出題傾向に変更が見られないので過去問で対策をとるのは非常に有効です。

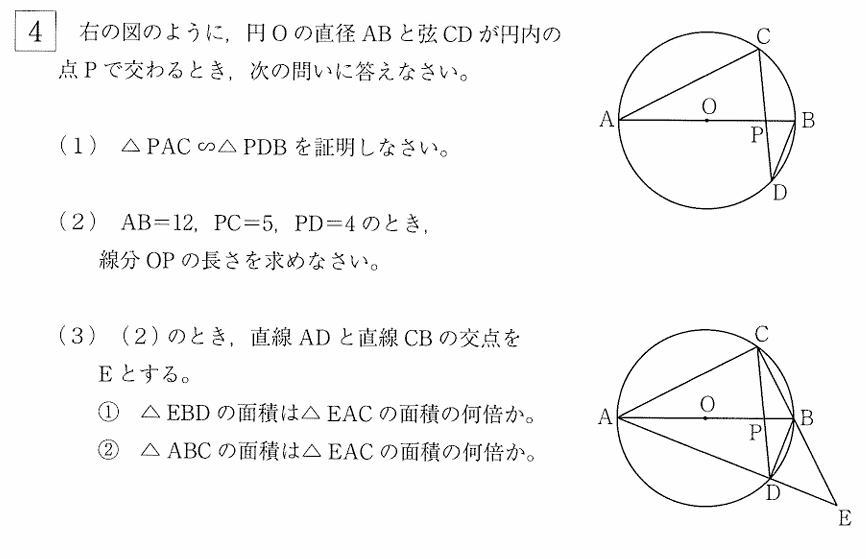
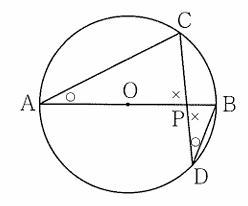
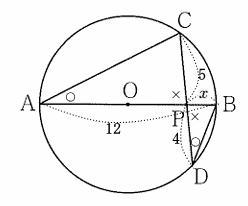
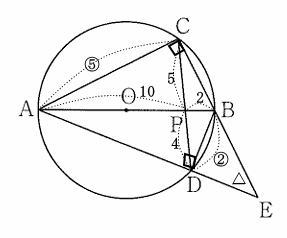
今回は　４.平面図形(円の性質と相似形)を解説します。

国学院大学久我山高校2025年度数学入試問題4.平面図形(円の性質と相似形) 問題

国学院大学久我山高校2025年度数学入試問題2.平面図形(円の性質と相似形) (1)解説解答

(1)　△PAC ∽ △PDBを証明しなさい。

解説解答

∠ACPと∠DBPは弧ADの円周角で等しい。

∠PACと∠PDBは弧BCの円周角で等しい。

∠CPAと∠BPDは対頂角で等しい。　この３つの等しい条件のうち２つの角が等しいことを用いて相似であることを証明します。

証明
△PACと △PDBにおいて

∠CPA = ∠BPD (対頂角)

∠PAC = ∠PDB (弧BCの円周角)

２組の角がそれぞれ等しいので　△PAC ∽ △PDB

国学院大学久我山高校2025年度数学入試問題2.平面図形(円の性質と相似形) (2)解説解答

(2)　AB = 12，PC = 5，PD = 4のとき、線分OPの長さを求めなさい。

解説解答

(1)より△PAC ∽ △PDBなので　PA：PD = CP：BP

国学院大学久我山高校2025年度数学入試問題2.平面図形(円の性質と相似形) (3)①解説解答

(3)　(2)のとき、直線ADと直線CBの交点をEとする。

①　△EBDの面積は△EACの面積の何倍か。

解説解答

△ECAと△EDBにおいて

∠ECA = ∠ADB = 90° 　(直径の円周角)
∠EDB = 180° - ∠ADB = 180° - 90° = 90°
よって　∠ECA = ∠EDB
∠AEC = ∠BED　(共通) 　　2角相等なので　△ECA ∽ △EDB
(1)　より　CP：BD　≠５:2なので　CA：DB　= 5：2

国学院大学久我山高校2025年度数学入試問題2.平面図形(円の性質と相似形) (3)②解説解答

②　△ABCの面積は△EACの面積の何倍か。

解説解答

①より△EACの面積を[25]，△EDBの面積を[4]とする。四角形BCADの面積は[25] - [4] = [21]

△ABCと△ABDは底辺が等しいので　辺の比 = 面積比はPC：PD = 5：4

國學院大學久我山高校数学入試問題解説解答 高校受験はプロ家庭教師集団スペースONEにお任せください。