九州国際大附属高等学校数学過去問研究
2013年度 九州国際大附属高校一般算数入学試験問題は 例年通り 小問集合と大問5題の構成でした。出題内容は 1.計算を含む小問集合10問 2.関数のグラフ 3.規則性と立体の体積・表面積 4.方程式の応用 5.平面図形(円の性質) 6.平面図形と立体図形でした。
難問はなく、各分野から基本~標準レベルの問題が満遍なく出題されていました。
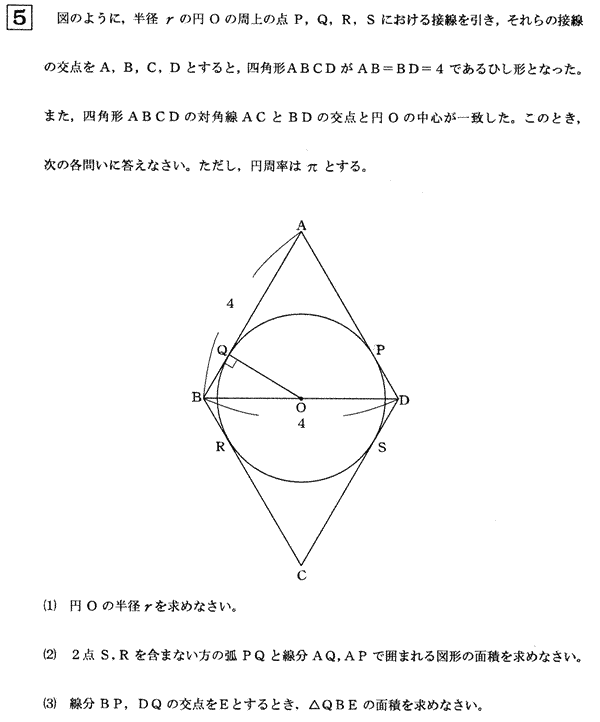
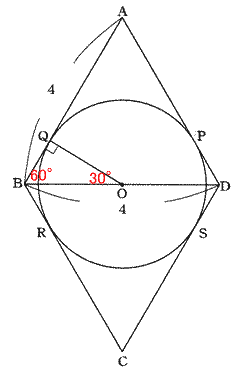
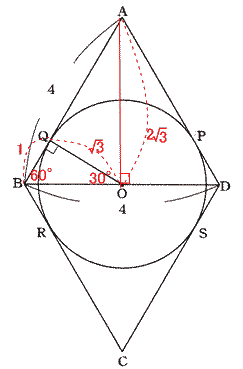
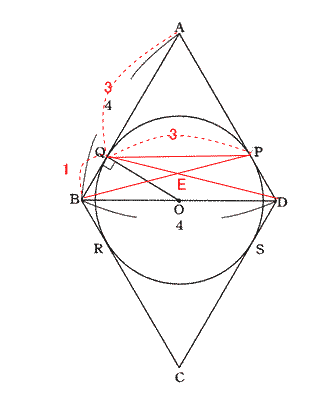
今回は 5.平面図形(円の性質)を解説します。三平方の定理を用いた出題です。要領よく補助線を引いて 各角度が30°,60°の直角三角形を見つけていきましょう。