
明治学院高等学校一般入試数学過去問研究
三角形の3辺に接する円をその三角形の内接円といい、その中心を内心といいます。内心と三角形の性質を理解しておくと、楽に解き進むことができます。
今回は2015年度明治学院東村山高等学校数学一般入試問題5を解説します。受験生の正答率は(1)37.3% (2)51.9% (3)33.0%でした。
今回は2015年度明治学院東村山高等学校数学一般入試問題5を解説します。受験生の正答率は(1)37.3% (2)51.9% (3)33.0%でした。

プロ家庭教師集団スペースONEプロの技術をご家庭にお届けします。私たちにお任せください。
電話: 03-4363-5472
090-3432-2593
受付時間: 平日 AM 10:00 〜 PM 9:00


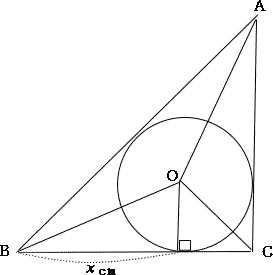
| (1) 円の半径を求めなさい。 |
| 解説解答 |
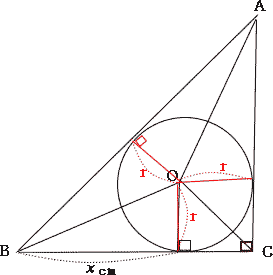 |
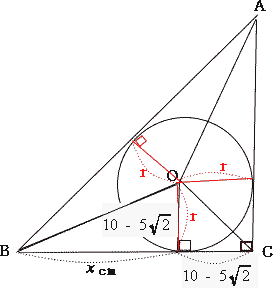
| 円の接線は、接点を通る半径に垂直なので、接点と内心を直線で結ぶと、 図の通り△ABO, △BCO, △CAOはともに辺AB, 辺BC, 辺CAを底辺とするときの高さが円の半径となる。 △ABCは直角二等辺三角形なので、 辺ABの長さは、三平方の定理より 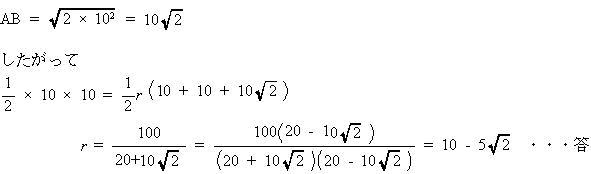 |
| 別解 |
 |
| (2) x の値を求めなさい。 |
| 解説解答 |
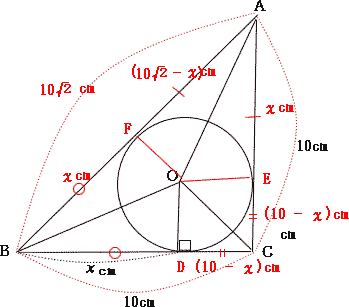 |
| 内心から辺AB,辺BC,辺CAに垂線を引きその交点をそれぞれF,D,Eとする。 円外の1点からその円にひいた2つの接線の長さは等しいので、 図の通り AF = AEより 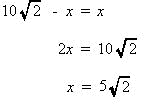 |
| (3) OC の長さを求めなさい。 |
| 解説解答 |
 |
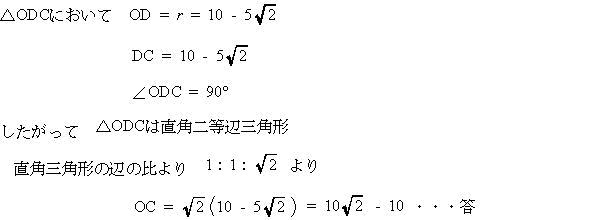 |