
明治学院高等学校過去問研究
明治学院高等学校の2015年度数学入試問題は大問5題構成で、出題内容は1.小問集合9問,2.確率,3.関数,4.一次方程式の応用,5.立体図形の展開図でした。
全体的に問題の分量・難易度ともに例年通りです。
過去問題を十分研究し問題傾向とボリュームになれて対策を取りましょう。
今回は 5.立体図形を解説します。

プロ家庭教師集団スペースONEプロの技術をご家庭にお届けします。私たちにお任せください。
電話: 03-4363-5472
090-3432-2593
受付時間: 平日 AM 10:00 〜 PM 9:00



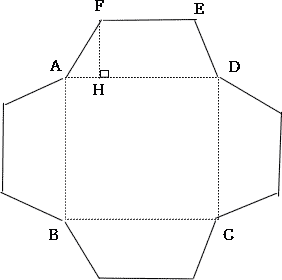
| (1) 辺FAの長さを求めよ。 |
| 解説解答 |
| 四角形ADEFは等脚台形なので、点Eから辺ADに垂線をおろし、その交点をIとする。 |
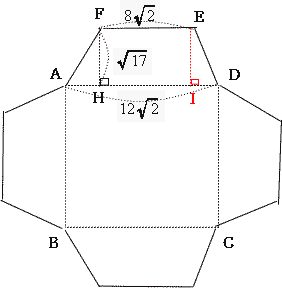 |
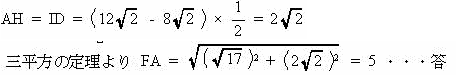 |
| (2) 立体の高さを求めよ。 |
| 解説解答 |
| 立体の見取り図は下図の通り |
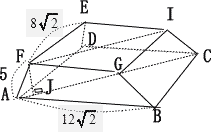 |
| 上底をEFGIとする。上底EFGIも下底ABCDも正方形でありAF = CIより、四角形ACIFは等脚台形 FIは正方形EFGIの対角線なので、 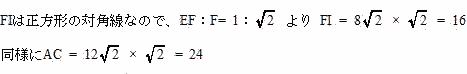 FからACに垂線をおろし、その交点をJとする。 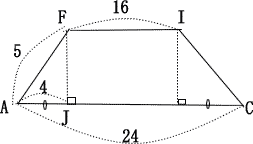 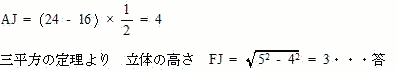 |
| (3) 立体の体積を求めよ。 |
| 解説解答 |
AF,BG,CI,DEを延長すると、1点で交わり、その交点をPとする。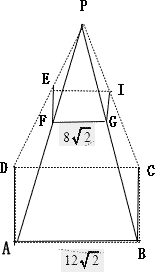 P-ABCDは正四角錐なので、求める体積は (正四角錐P-ABCD) - (正四角錐P-FGIE) 点Pから底面ABCDに垂線をおろしその交点をQとする。底面ABCDは正方形なので、Qは対角線AC,DBの交点であり、AC,DBの中点となる。 |
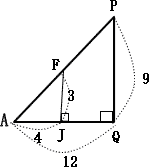 図の通り △AFJ ∽ △APQ より、AJ:AQ = 4:12 = 1:3 よって PQ = 9 |
 |
| 答 608 |