
土浦日本大学高等学校数学過去問研究
例年通りオールマークシート解答形式で、出題構成は大問5題、1.2.小問集合 3,確率 4.関数 5.立体図形でした。
今回は3.確率を解説します。一次関数の座標点との融合問題でした。

プロ家庭教師集団スペースONEプロの技術をご家庭にお届けします。私たちにお任せください。
電話: 03-4363-5472
090-3432-2593
お問い合わせ
受付時間: 平日 AM 10:00 〜 PM 9:00


例年通りオールマークシート解答形式で、出題構成は大問5題、1.2.小問集合 3,確率 4.関数 5.立体図形でした。
今回は3.確率を解説します。一次関数の座標点との融合問題でした。
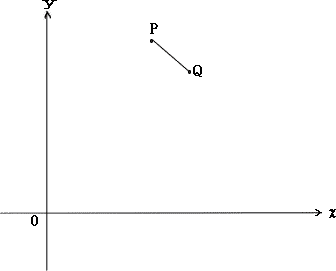
| 解説 |
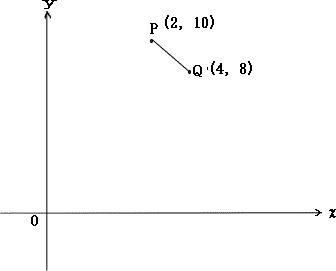 |
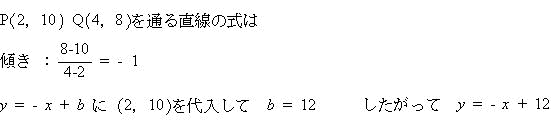 |
| aはサイコロの目なので 1 ≦ a ≦ 6, また y = aχとy = -χ + 12 との交点の範囲は 2≦χ≦4, 8 ≦ y ≦10 |
| a=1 のとき、y = χとy = -χ + 12 との交点は χ = -χ + 12 より χ = 6 |
| a=2 のとき、y = 2χとy = -χ + 12 との交点は 2χ = -χ + 12 より χ = 4 |
| a=3 のとき、y = 3χとy = -χ + 12 との交点は 3χ = -χ + 12 より χ = 3 |
| a=4 のとき、y = 4χとy = -χ + 12 との交点は 4χ = -χ + 12 より χ = 2.4 |
| a=5 のとき、y = 5χとy = -χ + 12 との交点は 5χ = -χ + 12 より χ = 2 |
| 以上より 関数 y = aχが線分PQとの交点を持つのは a = 2,3,4,5 の場合 |
| 別解 |
| P(2,10)なので y = aχのグラフが点Pを通るとき 10 = 2a より a = 5 |
| Q(4,8)なので y = aχのグラフが点Pを通るとき 8 = 4a より a = 2 |
| したがって a = 2,3,4,5 |
| 答 ア 2 イ 3 |
| (2) 1回目に投げたあとにもう1回サイコロを投げて、2回目に出た目の数をbとする。 |
| 解説 |
 |
 |
| 解説 |
| 原点と点Pを通る直線の傾きが1のとき、切片は 10 - 2 = 8 |
| 原点と点Qを通る直線の傾きが1のとき、切片は 8 - 4 = 4 |
| a = 2 のとき b = 6 |
| a = 3 のとき b = 5,6, |
| a = 4 のとき b = 4,5,6 |
| a = 5 のとき b = 3,4,5,6 |
| a = 6 のとき b = 2,3,4,5,6 計 15通り |
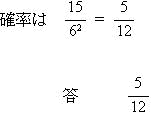 |