桜美林高等学校数学過去問研究
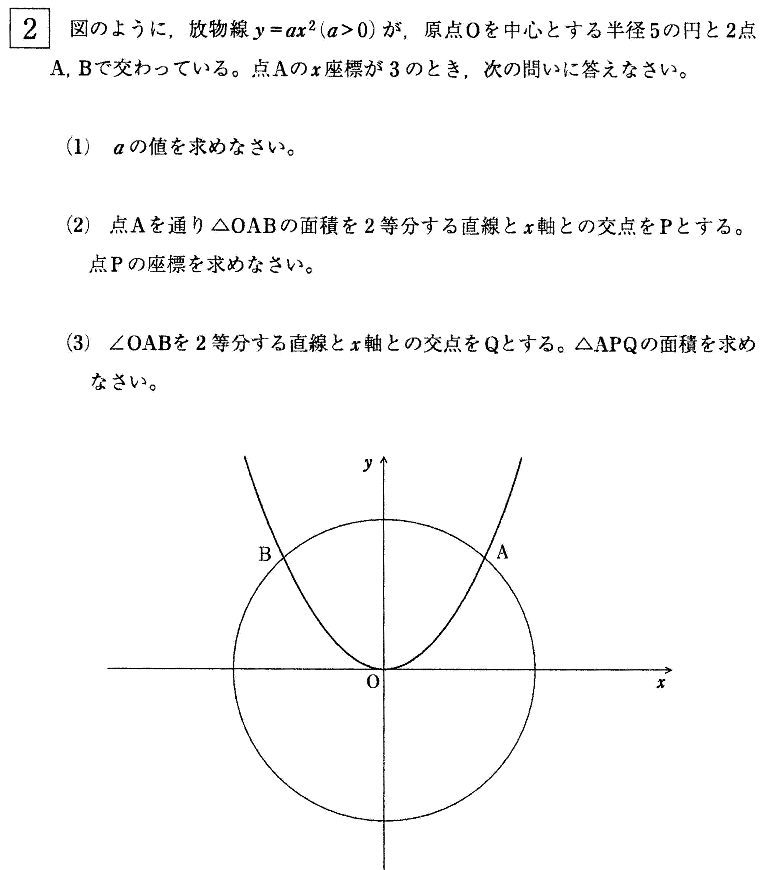
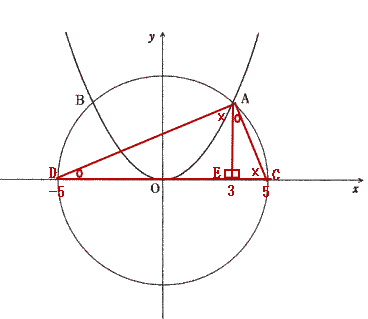
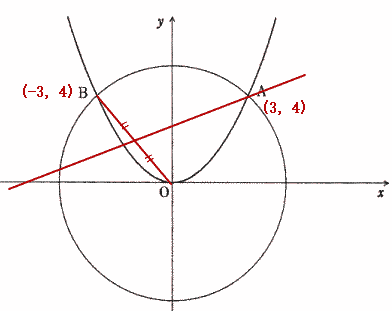
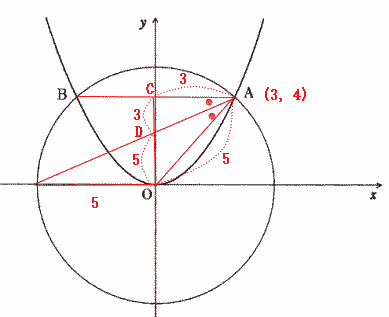
今回は 桜美林高校入試問題2の座標平面問題を解説します。(1) は 半径の長さを用いて相似比から求めましょう。(2)は中点の求め方の公式を用いて解きましょう。基本レベルですが、補助線の引き方がポイントです

プロ家庭教師集団スペースONEプロの技術をご家庭にお届けします。私たちにお任せください。
電話: 03-6868-6040
受付時間: 平日 AM 10:00 〜 PM 9:00


今回は 桜美林高校入試問題2の座標平面問題を解説します。(1) は 半径の長さを用いて相似比から求めましょう。(2)は中点の求め方の公式を用いて解きましょう。基本レベルですが、補助線の引き方がポイントです