埼玉県立高等学校共通入試問題過去問研究
2018年度埼玉県立高校前期共通数学入試問題は、例年通り大問4題構成。1.小問集合 11問 2.小問4問 3.規則性 4.関数のグラフが出題されました。
今回は3.規則性を解説します。奇数列であることに気がつけば、すぐ解ける問題です。
埼玉県立高校 過去問対策
有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。
埼玉県立高校数学入試問題 2018年度入試問題 3．規則性
(1) 解説解答
 |
| 解説解答 |
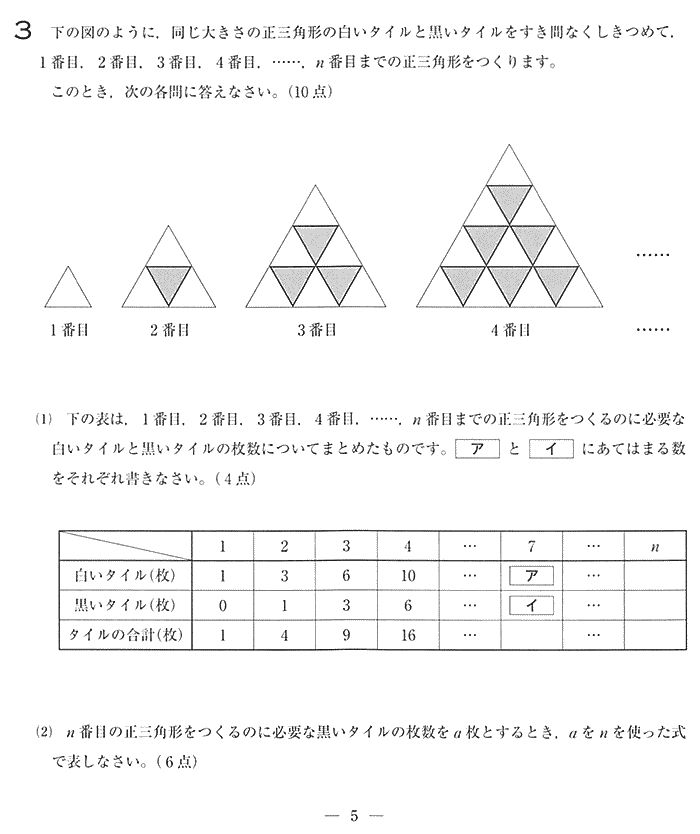
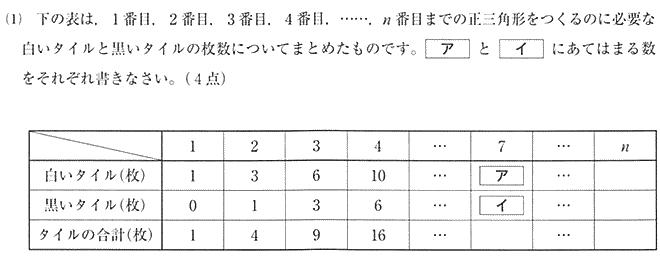
| 白いタイルは 1番目は1枚，2番目は 1 + 2 = 3枚， 3番目は 1 + 2 + 3 = 6枚と増えていくので、7番目は 1 + 2 +
3 + 4 + 5 + 6 + 7 = (1 + 7)×7÷2 = 28枚 タイルの合計は 1番目は 1×1 = 1，2番目は 2×2 = 4，3番目は 3×3 と奇数列の和なので、7番目のタイルの合計は 7×7 = 49枚 よって 黒いタイルの枚数は 49 - 28 = 21枚 別解 7番目の黒いタイルの枚数は 1 + 2 + ・・・・+ 6 = ( 1 + 6)×6÷2 = 21枚 |
| 答 ア 28， イ 21 |
(2) 解説解答
| (2) n番目の正三角形をつくるのに必要な黒いタイルの枚数をaとするとき、aをnを使った式で表しなさい。 |
| 解説解答 |
| 黒いタイルは 1番目は0，2番目は0 + 1，3番目は 0 + 1 + 2と増えていくので n番目のタイルの枚数は |
 |
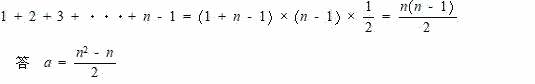