高校受験はプロ集団にお任せ/プロ家庭教師集団スペースＯＮＥの西南女学院高校2015年度数学入試問題平面図形

青山学院高等部数学入試問題出題傾向と解説解答
高校受験はスペースONEのプロ家庭教師にお任せください。

青山学院高等部過去問傾向と対策

西南女学院高等学校過去問研究

2015年度西南女学院高等学校の数学入試問題は　例年通りの出題構成で、１．小問集合　２．割合　３．立体図形(含証明問題)　４．関数のグラフ　５．立体図形　大問５題の出題でした。

１．は解答のみを解答欄に書く形式で、２～５．は途中式を書く解答形式でした。

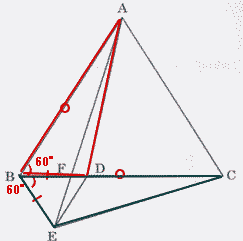
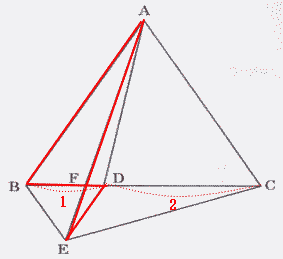
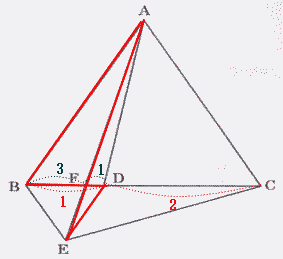
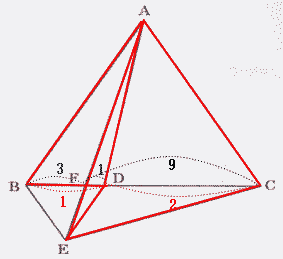
今回は　スペースONE福岡校のプロ家庭教師が　5. 平面図形を解説します。　

西南女学院高等学校2015年度数学入試問題5.平面図形問題

西南女学院高等学校2015年度数学入試問題5.平面図形 (1)解説解答

(1)　(1)　AD = CEであることを証明しなさい。

解説解答

△ABDと△CBEにおいて、過程より AB = CB, BD = BE,　∠ABD = ∠DBE = 60°

二辺とその間の角がそれぞれ等しいので　△ABD　≡　△CBE

したがって　AD = CE
　　

西南女学院高等学校2015年度数学入試問題5.平面図形 (2)解説解答

(2)　BD：DC = 1：2とするとき①　次の線分の比をもっとも簡単な整数の比で答えなさい。

解説解答

(ア) 　AF：FE解説△FABと△FEDにおいて、

∠BFA = ∠DFE (対頂角)

∠ABF = ∠EDF = 60°

二角相等なので　△FAB ∽ △FED

よって　FA：FE = AB：ED

BD：DC = 1：2なので　AB：ED = BD + DC：BD = 1 + 2：1 = 3：1

したがって　AF：FE = 3：1答　　3：1

西南女学院高等学校2015年度数学入試問題5.平面図形問題 (3)解説解答

(イ) 　ＢＦ：ＦＤ：ＤＣ

解説

(ア) △FAB ∽ △FEDより　ＢＦ：ＤＦ = ３：１

BD：DC = 1：2なので

②　四角形ABECの面積は△ADEの面積の何倍かを求めなさい。

解説

△AEDと△AECは底辺AEが共通なので、高さの比 = 面積比になるから

ＦＤ：ＦＣ = 1：1 + 8 = 1：9

よって　△AED：△AEC = 1：9 ・・・①

また△AEDと△ABEは底辺AEが共通なので、高さの比 = 面積比になるから

ＦＤ：ＦB = 1：3

よって　△AED：△ABE = 1：3　・・・②

①，②より

△AED：△AEC：△ABE = 1：9：3

△AED：四角形ABEC = △AED：△AEC + △ABE = 1：9 + 3 = 1 ： 12

したがって四角形ABECの面積は△ADEの面積の12倍

答　　12倍

青山学院高等部数学入試問題出題傾向と解説解答 高校受験はスペースONEのプロ家庭教師にお任せください。