専修大学付属高等学校過去問研究
専修大学付属高等学校の2008年度数学入試問題は小問集合７題、大問４題構成でした。
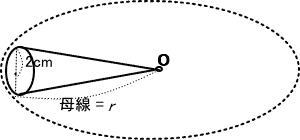
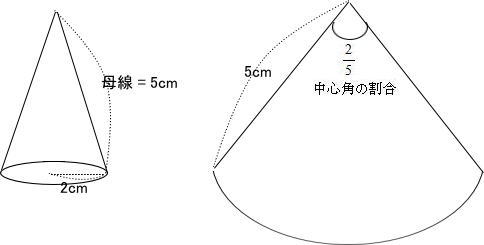
専修大学付属高等学校の数学入試問題では平面図形（座標平面を含む）が頻出です。多角形・円の性質、相似合同条件は繰り返し練習しましょう。
専修大学付属高校 過去問傾向と対策
有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。
専修大学附属高校2008年度数学入試問題 円錐の回転図形 問題
図のように底面の半径が2cmの円錐を頂点Ｏを中心として平面上で転がした。
すると円錐は点線で示した円の上を１周して元の場所に戻るまでに、ちょうど２回半回転した。
次の各問に答えなさい。
① 円錐の母線の長さを求めなさい。
② 円錐の表面積を求めなさい。
専修大学附属高校2008年度数学入試問題 円錐の回転図形① 解説解答
解説
円錐の母線の長さ = 円Oの半径
円錐は点線で示した円の上を1周して元の場所に戻るまでに、ちょうど2回半回転したので、
円Oの円周は 円錐の直径の2.5倍 円錐の直径は4πなので
4π×2.5 = 2rπ
円Oの円周は 円錐の直径の2.5倍 円錐の直径は4πなので
4π×2.5 = 2rπ
ｒ = 5
答 5cm
答 5cm
専修大学附属高校2008年度数学入試問題 円錐の回転図形 ② 解説解答
② 円錐の表面積を求めなさい。
解説解答
側面積(扇形)の面積は
半径5cm，
なので
よって 円錐の表面積 = 側面積の面積 + 半径2cmの円の面積なので
答 14π
