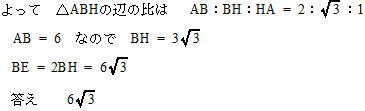高校受験はプロにお任せ/プロ家庭教師集団スペースＯＮＥの品川翔英高校2025年度数学入試問題平面図形

品川翔英高校入試問題傾向と対策
高校受験指導はスペースONEのプロ家庭教師にお任せください。

品川翔英高校　過去問解説解答

品川翔英高等学校一般入試問題数学過去問対策

小野学園中学高等学校は2020年に校名を品川翔英中学校・高等学校に変更し、女子校から共学校になりました。

2025年度品川翔英高校一般数学入試問題は、大問5題構成で、1.四則演算を含む小問集合10問(配点合計40点)　2.二次関数のグラフ問題(配点合計15点)　3.空間図形の切断問題(配点合計15点)　4.平面図形(証明問題を含む平行四辺形の性質)(配点合計15点)　5.確率(配点合計15点)が出題されました。

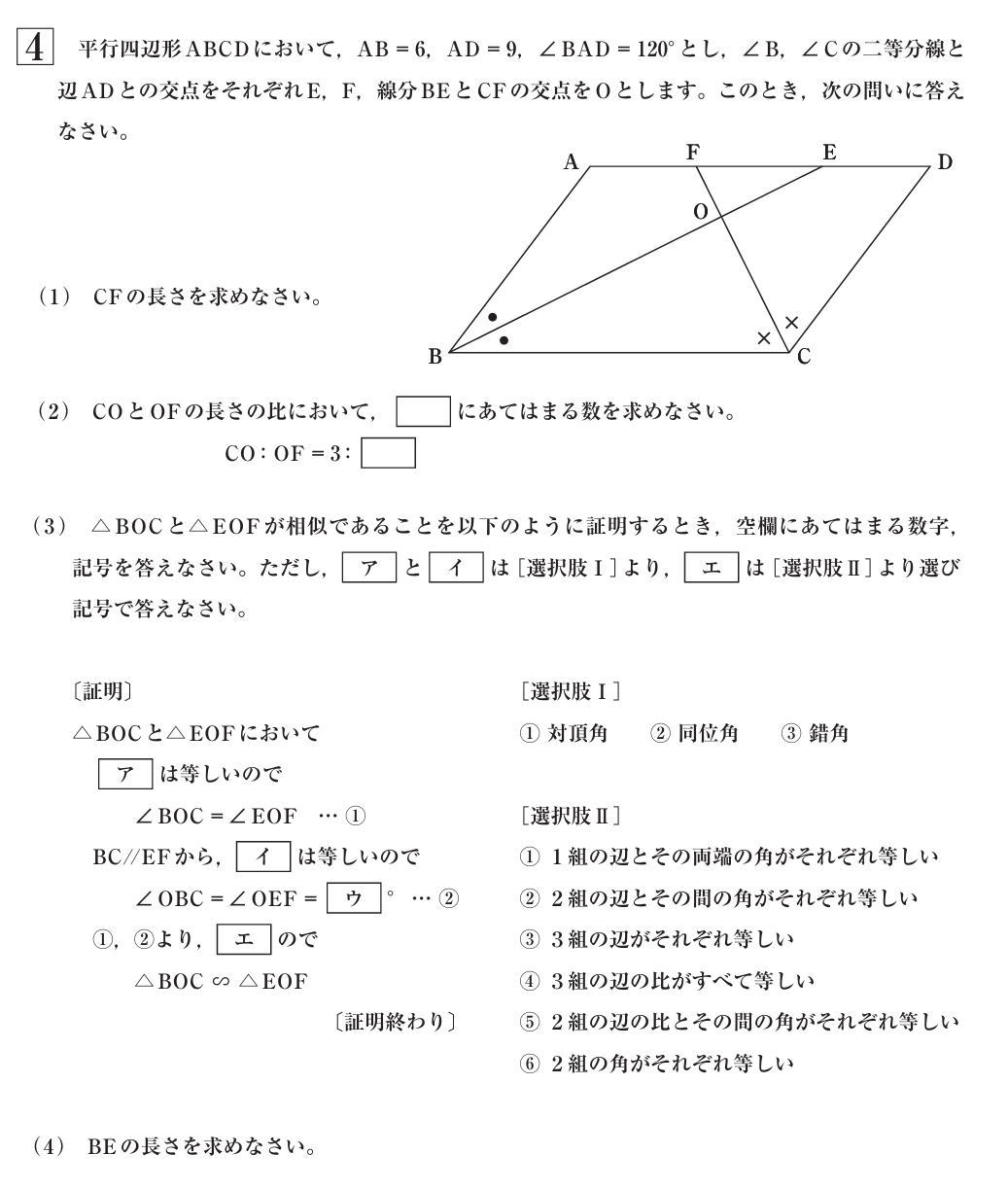
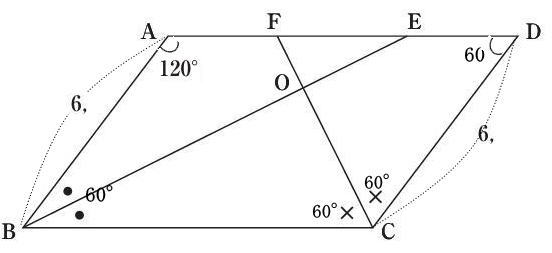
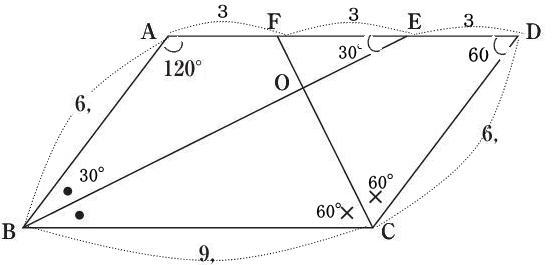
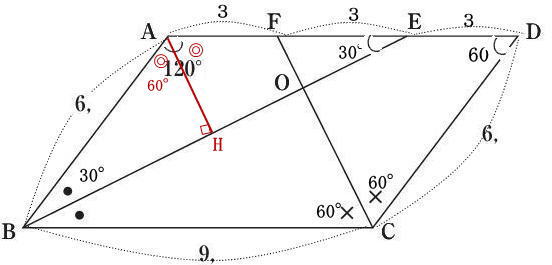
今回は4.平面図形を解説します。

品川翔英高校2025年度一般数学入試問題4.平面図形問題

品川翔英高校2025年度一般数学入試問題4.平面図形 (1)解説解答

(1)　CFの長さを求めなさい。

解説解答

平行四辺形の性質より　∠DAB = ∠BCD = 120°

線分CFは∠BCDの二等分線なので　∠BCF = ∠FCD = 60° ・・・①

平行四辺形の性質より　∠DAB + ∠ABC = 180°

∠ABC = 180° - 120° = 60°

∠ABC = ∠CDA = 60°・・・②

①，②より　△CFDは正三角形

したがって　CF = FD = DC = 6

答え　　　6

品川翔英高校2025年度一般数学入試問題4.平面図形 (2)解説解答

(2) 　COとOFの長さの比において、□にあてはまる数を求めなさい。

　　　CO：OF = 3：□

解説解答

(1)より　FD = 6　よってAF = 9 - 6 = 3・・・①

△ABEにおいて　BEは∠ABCの二等分線なので　∠ABE = 60÷2 = 30°

∠BEA = 180° - (120° + 30°)= 30°

したがって△ABEは二等辺三角形なので　AB = AE = 6

よって　ED = AD　‐AE = 9 - 6 = 3・・・②

①，②より　FE = AD - (AF + ED) = 9 - 3×2 = 3

AD // BCなので　△BOC ∽ △FOE

BC：EF = CO：OF = 9：3 = 3：1

答え　　1

品川翔英高校2025年度一般数学入試問題4.平面図形 (3)解説解答

(3) 　△BOCと△EOFが相似形であることを以下のように証明するとき、空欄にあてはまる数字、記号を答えなさい。

証明　

△BOCと△EOFにおいて　[ア]は等しいので　
∠BOC = ∠EOF・・・①
BC//EFから、[イ]は等しいので　
∠OBC = ∠OEF = [ウ]・・・②
①，②より　[エ]ので　△BOC ∽ △EOF　[証明終わり]　

解説解答

△BOCと△EOFは対頂角で等しい。

∠OBC と ∠OEFは平行線の錯角なので　等しい。△ABEにおいて　BEは∠ABCの二等分線なので　∠ABE = 60÷2 = 30°

よって　∠OBC = ∠OEF = 30°

△BOCと△EOFは二角相等なので相似形になる。

答え　　　[ア]　①　 [イ]　③　 [ウ]　30　 [エ]　⑥

品川翔英高校2025年度一般数学入試問題4.平面図形 (4)解説解答

(4)　BEの長さを求めなさい。

解説解答

∠EABの二等分線を線分BEにおろしその交点をHとする。

二等辺三角形において頂角の二等分線は底辺を垂直に二等分するので　∠BHA = ∠AHE = 90°　BH = HE

品川翔英高校入試問題傾向と対策 高校受験指導はスペースONEのプロ家庭教師にお任せください。

品川翔英高校 過去問解説解答