立教新座高等学校過去問研究
2009年度立教新座高等学校受験者数1,245名 合格者 620名 補欠者数 128名 補欠繰り上げ数 93名 実質倍率 1.75倍でした。
立教新座高等学校の2009年度数学入試問題は小問集6題、大問5題構成でした。昨年より小問が1問増え、この一問がかなりの難問でしたので、ここに時間をとられ時間配分をうまく調節できなかった受験生もいたようです。
立教新座高等学校の2009年度数学入試問題は小問集6題、大問5題構成でした。昨年より小問が1問増え、この一問がかなりの難問でしたので、ここに時間をとられ時間配分をうまく調節できなかった受験生もいたようです。
ここ数年難易度が高くなっていますが、今年はさらに難化しています。
2010年度の入試日は 2月2日 あと残すところ約80日
過去問題を十分研究したうえ問題傾向より難易度の高い問題にも取り組みましょう。
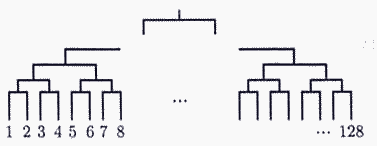
今回は小問集合の中から難問の(6)と立教新座高等学校としては珍しい4のトーナメントを扱った問題を解説します。