有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。
都立八王子東高校 過去問対策

東京都立八王子東高等学校過去問研究
(1)は円周角・内角・外角・外接の基本を確認しましょう。(2)の問題は都立トップ校らしいひねりのきいた難問です。(3)は受験必修の証明問題です。
数学独自入試問題
都立八王子東高校2008年度独自作成数学考査問題3.平面図形 問2解説解答
平面図形の問題では、三平方の定理、相似形にポイントが絞られます。
相似形は補助線をどこに引くかが肝心です。
この問題では、もう一点「円の接線は接点をとおる半径に垂直である」の円の接線の性質も確認しましょう。
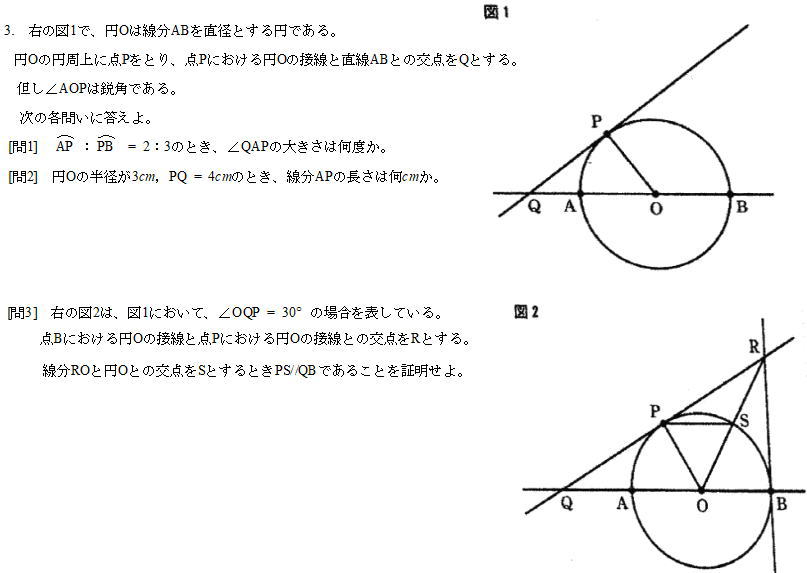
問2
円Oの半径が3cm、PQ=4cmのとき、線分APの長さは何cmか。
解説解答
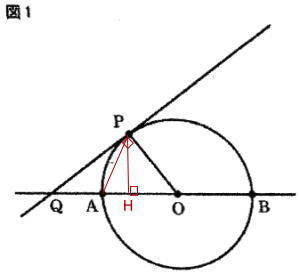
点Pから線分QBに垂線を引き、交点をHとする。
∠QPO=∠PHO=∠90°
∠POQ=∠POH・・・共通
よって三角形の2つの角が等しいので、△QPO∽△HPO
△QPOにおいて 辺PQ=4cm 辺PO=3cm の直角三角形なので、
三平方の定理より
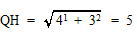
HP:PO:OH=4:5:3 PO=3cmなので
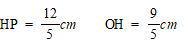
また △PAHは ∠PHA = ∠90° の直角三角形。
三平方の定理より
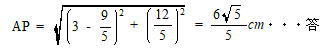
まずはじめに証明するために必要な条件を確認しましょう。
平行条件(①錯角が等しい ②同位角が等しい)
円周角と接線の性質(①円以外の1点からその円に引いた2つの接線の長さは等しい ②円の接線は接点をとおる半径に垂直である)
以上の条件を用いて証明問題を解きましょう。
高校受験の証明問題では2つの三角形の相似または合同であることとから導くことが一般的ですね。
問3
右の図2は、図1において、∠OQP=30°の場合を表している。
点Bにおける円Oの接線と点Pにおける円Oの接線との交点をRとする。
線分ROと円Oとの交点をSとするとき、PS//QBであることを証明せよ。
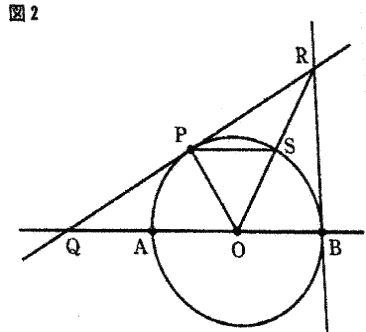
(証明)
△OPQにおいて、∠OQP =30°、∠OPQ = ∠R なので ∠POQ =
∠60°・・・①
△RPOと△RBOにおいて直線PR,BRは円Oの接線だから、∠RPO =∠RBO =
∠R・・・②
PO = BO (半径)・・・③
ROは共通・・・④
②③④より直角三角製の斜辺と他の一辺がそれぞれ等しいので、△RPO≡△RBO
よって、 ∠ROP = ∠ROB・・・⑤
①から、∠POB = 120°なので、⑤より、∠ROP = 60°OS = OP
(半径)より、
△OPSは正三角形となるので、∠SPO = 60°・・・⑥
①、⑥より、錯覚が等しいので、PS//QB