都立高校受験はプロ集団にお任せ/プロ家庭教師集団スペースＯＮＥの都立高校2021年度共通数学入試問題平面図形

都立高校入試過去問傾向と対策
高校受験指導はプロ家庭教師集団スペースONEにお任せください。

共通数学入試問題　　関数のグラフ3

右の図１で、点Oは原点、曲線 l は関数y＝χ²　のグラフを表している。点A,　点Bはともに曲線 l 上にあり、座標はそとのれぞれ（－６，９），（６，９）である。点Aと点Bを結ぶ。曲線 l 上にあり、ｘ座標がー６より大きく６より小さい数である点をPとする。点Pを通りｙ軸に平行な曲線を引き線分ABとの交点をQとする。座標軸の１目盛りを１ｃｍとして、次の各問に答えよ。［問１］　点Pのｘ座標をa,線分PQの長さをbｃｍとする。aのとる値の範囲が　　　－４＜ a ＜３　　のとき bのとる値の範囲を不等号を使って表せ。

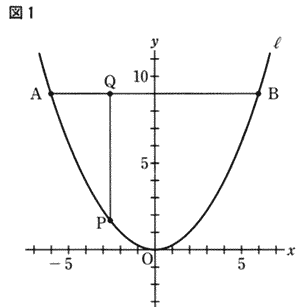[問２]　図２は、図１において、点Pのχ座標が正のとき、点Aと点Pを結び、線分APとｙ軸との交点をRとし、点Qと点R,点Bと点Pをそれぞれ結んだ場合を表している。次の①，②に答えよ。 ①　点Rの座標が（０，１）のとき，２点A，Pを通る直線の式を求めよ。 ②　PQ=AQとなるとき，△PBAの面積の何分のいくつか。

［問１］　点Pのｘ座標をa,線分PQの長さをbｃｍとする。aのとる値の範囲が　　　－４＜ a ＜３　　のとき bのとる値の範囲を不等号を使って表せ。

解説　　
点Pのｘ座標がaなので　ｙ座標は　ｙ＝a²　　

a=-4　のとき　ｙ＝・（－４）・（－４）＝４　よって　ｂ＝９－４＝５　　

a=３　のとき　ｙ＝・３・３＝9/4　よって　ｂ＝９－9/4＝27/4　　

答　５≦ ｂ ≦27/4

①　点Rの座標が（０，１）のとき，２点A，Pを通る直線の式を求めよ。

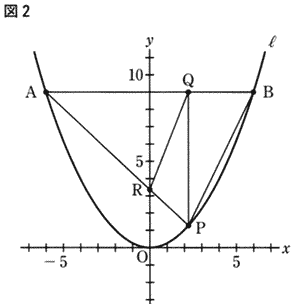	解説
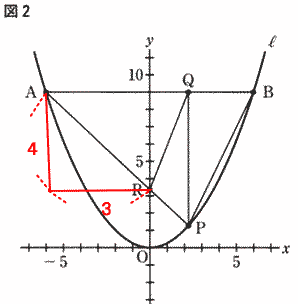	直線ARの傾きは　グラフより　－切片は　R座標（０,１）より　１　よって　APを通る直線の式はｙ＝－x＋１

②　PQ=AQとなるとき，△PBAの面積の何分のいくつか。

	解説
	PQ=AQとなるときの　点Q，点Pのｘ座標を　aとすると、点Qの座標は（a，９）点Pの座標は（a，９－a－６）＝（a，ーa＋３）　点Pは関数　y＝χ²　上の点なので、この式に（a，ーa＋３）を代入して a²＋４a－１２＝０　（a＋６）（a－２）＝０　 a＞０より　a＝２　Q（２，９）　P（２，２） △RPQの面積：△PBAの面積＝（９－２）×２÷２：６×２×（９－２）÷２＝１：６　　答　1/6