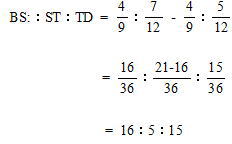東京都立高等学校共通数学過去問研究
東京都立の公立中高一貫校10校のうち、併設型の高等学校・附属中学校として設置されていた5校のうち、武蔵・富士・両国・大泉の4校が、2022年までに高校募集を停止し、中学募集の規模を拡大する計画が、2019年年2月14日付けで東京都教育委員会から「都立高校改革推進計画・新実施計画(第二次)」でプレスリリースされました。
この年次計画の表中では、「2021年度入学生から」の改編予定に、富士と武蔵、翌「2022年度入学生から」の改編予定に、両国、大泉の2校が挙げられており、欄外の注記の形で、「※白鷗高校・附属中学校については、施設設備の状況を踏まえて実施時期を決定(実施時期:平成33(2021)年度以降を予定)と付記されています。
2021年には、都立富士と都立武蔵が募集停止し、2022年には都立両国と都立大泉の各附属中学校が高校募集を停止し完全中高一貫校になりました。
都立高校数学出題の方針は
1 数量や図形などに関する基礎的・基本的な事項についての知識及び技能をみると ともに,これらを活用して問題を解決するために必要な数学的な思考力,判断力,
表現力等をみる。
2 1 数と式,図形,データの活用の各領域に関する基礎的・基本的な事項について の知識及び技能をみる。 2 数学的活動の場面をもとに,数学的な見方・考え方を働かせ,事象を数理的に 考察し処理する能力や,推論の過程を的確に表現する能力をみる。
3 関数についての知識及び技能をみるとともに,関数関係を表現し,見通しをも って論理的に考察し処理する能力をみる。
4 平面図形についての知識及び技能をみるとともに,見通しをもって論理的に考 察し処理する能力や,推論の過程を的確に表現する能力をみる。
5 空間図形についての知識及び技能をみるとともに,図形の性質や関係を直観的 に捉え,見通しをもって論理的に考察し処理する能力をみる。
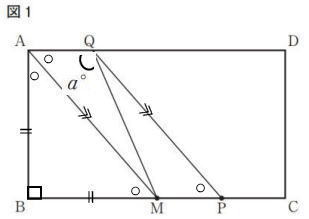
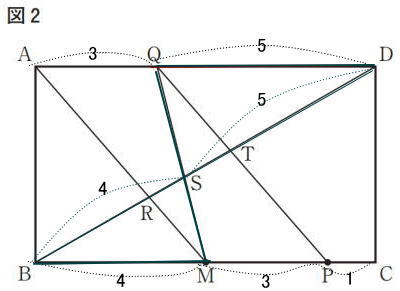
今回は4.相似形と辺の比を解説します。