都立高校入試過去問傾向と対策
高校受験指導はプロ家庭教師集団スペースONEにお任せください。
都立高校 過去問対策

東京都立高等学校共通数学過去問研究
令和7年度の東京都立高校の入学者選抜試験は2月21日に実施され、全日制は募集人員に対して約1・20倍の3万5877人が受験しました。
受東京都教育委員会発表の2025年度数学出題の方針は
数量や図形などに関する基礎的・基本的な事項についての知識及び技能を見るとともに、これらを活用して問題を解決するために必要な数学的な思考力・判断力・表現力を見る。
各問のねらい
4 平面図形についての知識及び技能をみるとともに,見通しをもって論理的に考 察し処理する能力や,推論の過程を的確に表現する能力をみる。
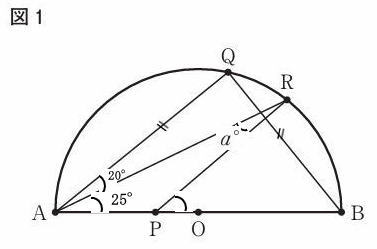
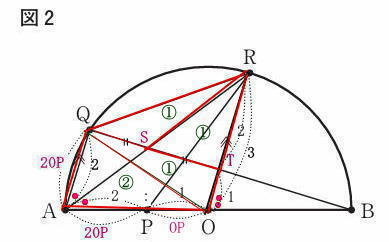
都立高校2025年度共通数学考査問題4.平面図形 問2①解説解答
問2
① △APR≡△AQRであることを証明せよ。
三角形の合同条件
・3組の辺がそれぞれ等しい。
・2組の辺とその間の角がそれぞれ等しい。
・1組の辺とその両端の角がそれぞれ等しい。
この合同条件のうち1つを満たせば、2つの三角形は合同であるといえる。
証明
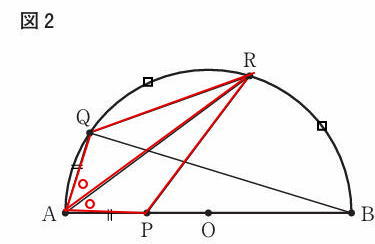
△APRと△AQRにおいて
AP = AQ (仮定)・・・①
AR = AR (共通)・・・②
弧BR = 弧QR(仮定)より 長さの等しい弧の円周角の大きさは等しいので
∠BAR = ∠RAQ・・・③
①,②,③より2組の辺とその間の角がそれぞれ等しいので
△APR ≡ △AQR
(証明終わり)