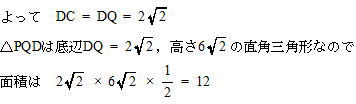都立国立高校 過去問対策
有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。
都立国立高校2008年度数学入試問題1.平面図形 問題
下の図１で、三角形ABCは、AB = BC = 8cm、∠ABC = 90°の直角三角形である。
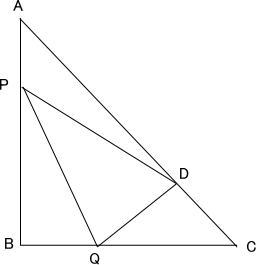
点Dは、辺AC上にある点で、AD：DC = 3：1である。
点Pは、辺AB上を頂点Aから頂点Bまで動く点である。
点Pと点Dを結ぶ。
点Dを通り線分PDに垂直な直線をひき、辺BCとの交点をQとする。
点Pと点Qを結ぶ。
次の問に答えなさい。
点Ｐが頂点Ａと一致するとき三角形PDQの面積は何c㎡か。
点Ｐが頂点Ａと一致するとき三角形PDQの面積は何c㎡か。
都立国立高校2008年度数学入試問題1.平面図形 解説解答
辺ＡＣの長さは△ＡＢＣが直角二等辺三角形なので、辺の比より
ＡＤ：ＤＣ＝３：１なので、
また、∠ＣＤＱ＝90°, ∠ＤCＱ = 45°なので、△DCQDQCは二等辺三角形、
答 12c㎡
