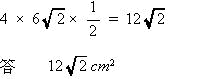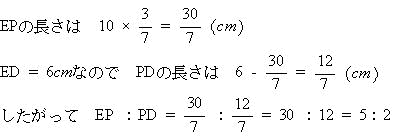東京都立進学重視型単位制高校数学過去問研究
2014年度から都立新宿,墨田川,国分寺高校が進学重視型単位制校として、共通の問題を出題するようになりました。大問4題構成で、[1」は各校独自の小問集合 [2]~[4]が3校共通問題でした。
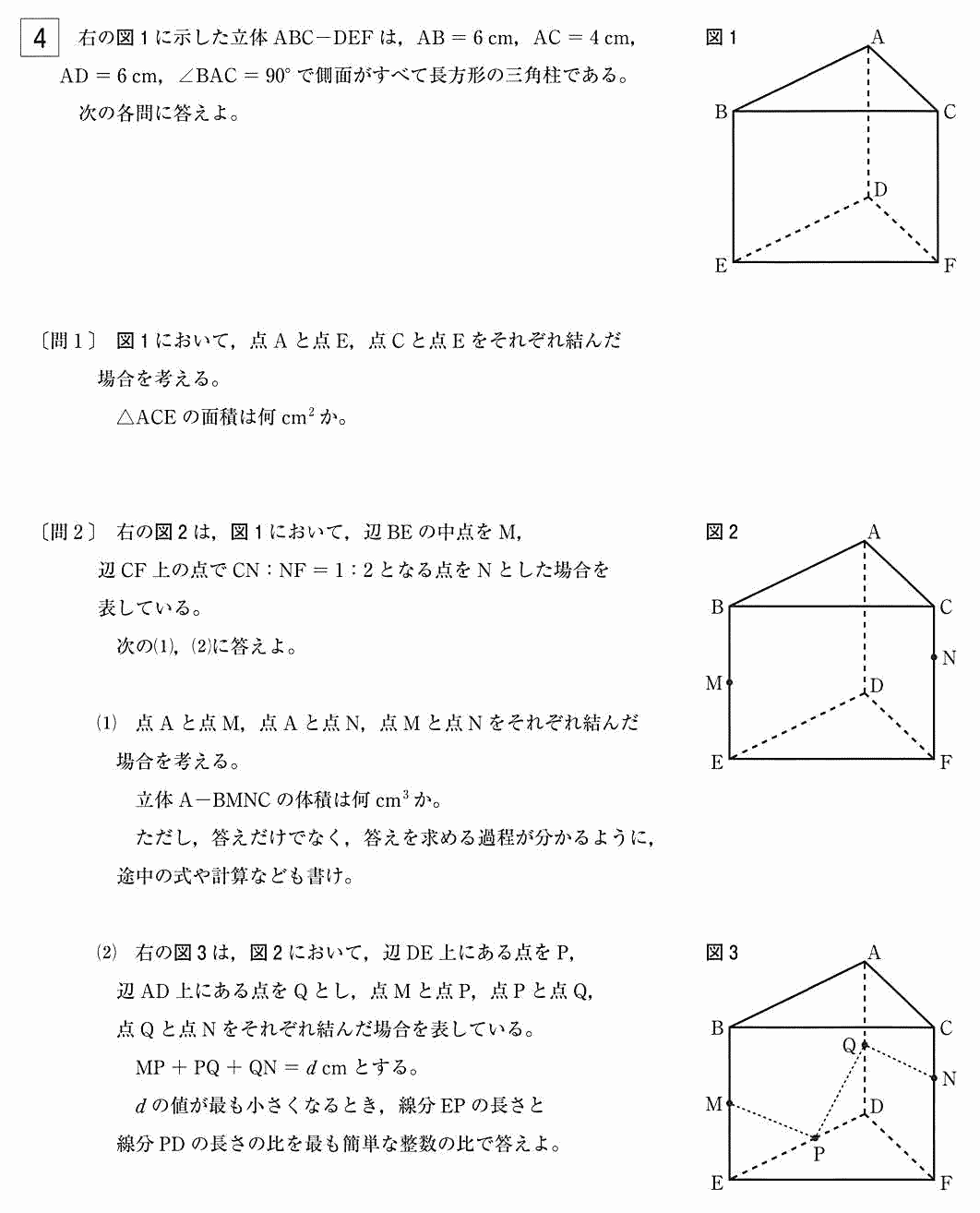
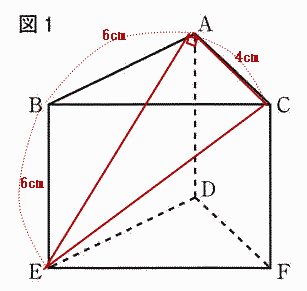
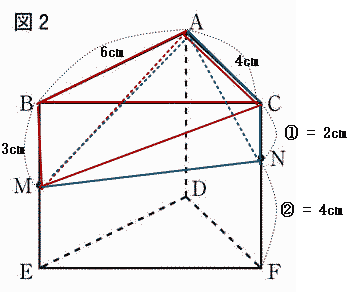
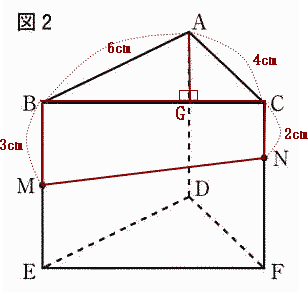
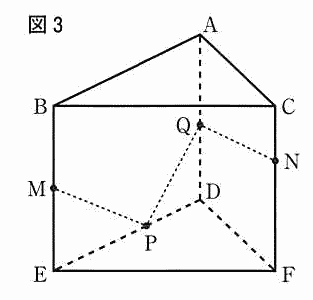
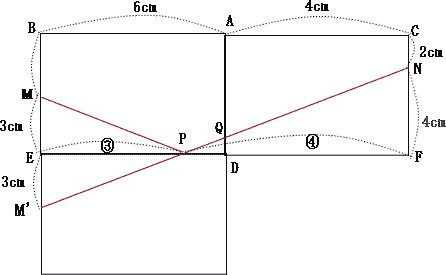
今回は[4]の立体図形を解説します。

プロ家庭教師集団スペースONEプロの技術をご家庭にお届けします。私たちにお任せください。
電話: 03-4363-5472
090-3432-2593
受付時間: 平日 AM 10:00 〜 PM 9:00


2014年度から都立新宿,墨田川,国分寺高校が進学重視型単位制校として、共通の問題を出題するようになりました。大問4題構成で、[1」は各校独自の小問集合 [2]~[4]が3校共通問題でした。
今回は[4]の立体図形を解説します。