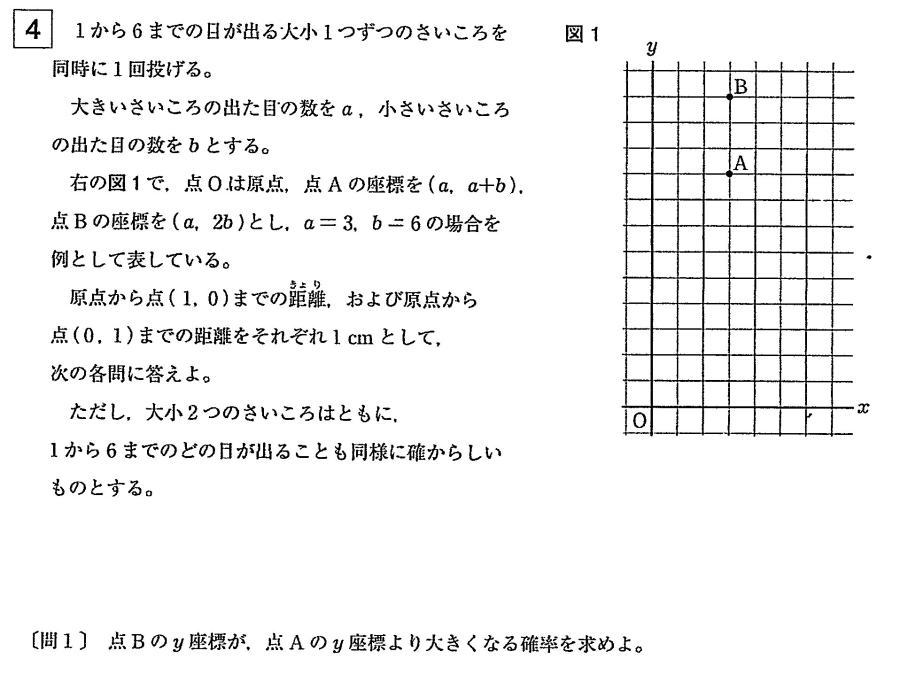
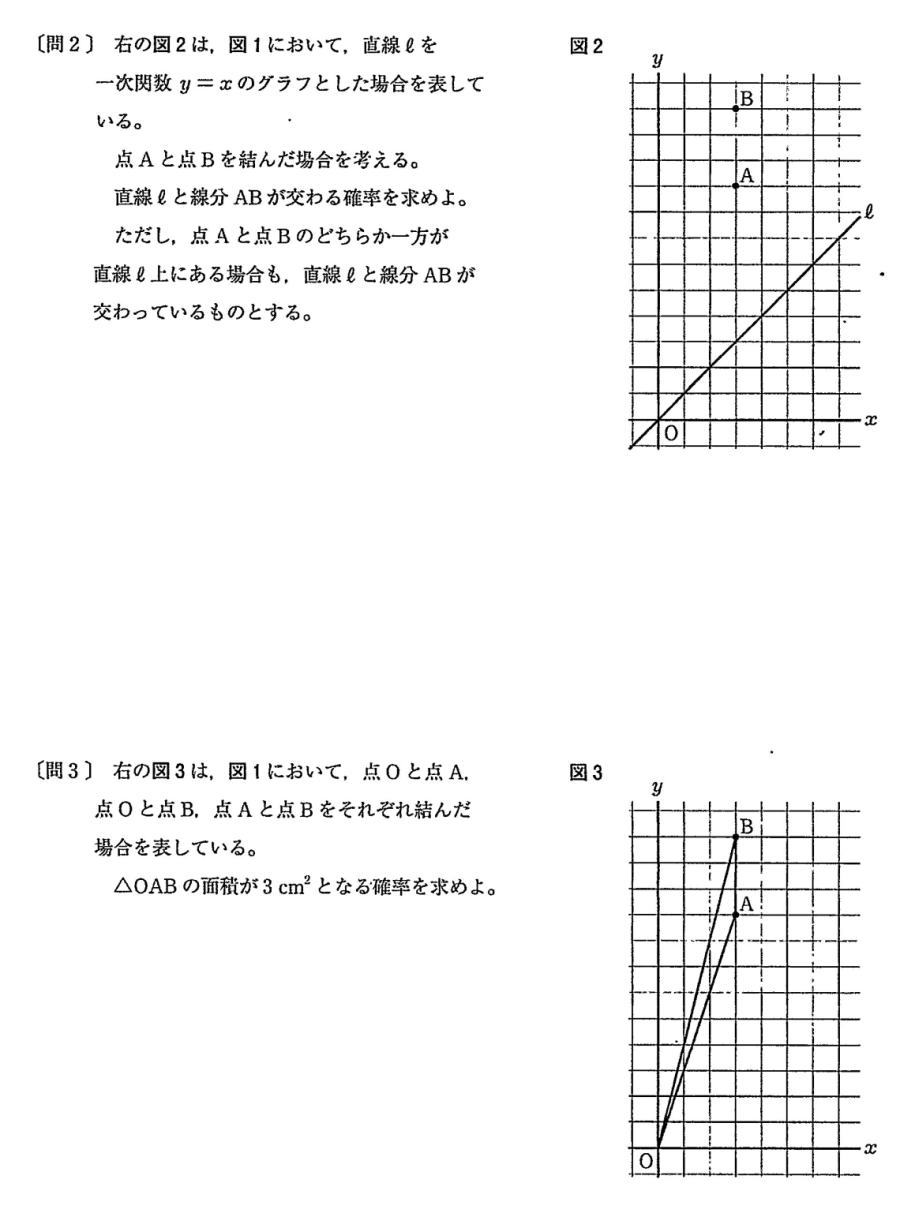
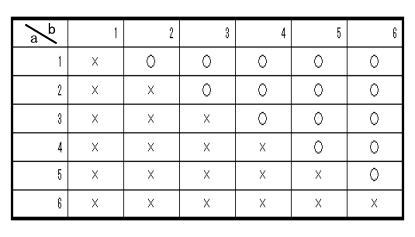
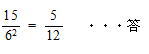高校受験はプロにお任せ/プロ家庭教師集団スペースＯＮＥの都立新宿高校2021年度数学入試問題場合の数と確率

有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、
多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。

都立新宿高校　過去問対策

東京都立新宿高等学校過去問研究

2021年度都立新宿高等学校は、推薦入試募集人数男女32名に対し、応募者男子41名，女子106名，合格者数男子8名，女子24名でした。

学力権者による入学者は、募集人数男女284名に対し、受験者数男子240名　女子247名，合格者数男子142名，女子146名でした。

独自数学入試問題は1.小問集合6問，２．関数のグラフ　３．平面図形(証明問題を含む)　４．場合の数と確率でした。

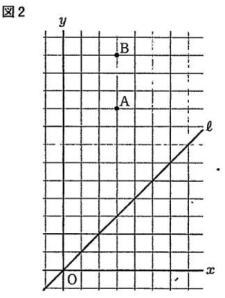
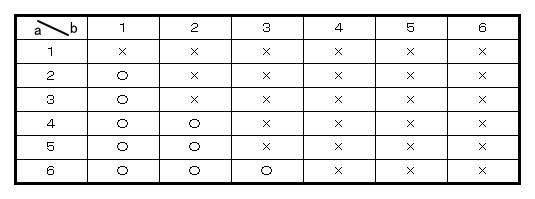
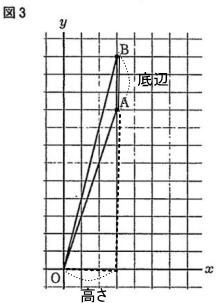
今回は４　場合の数と確率を解説します。数え上げは表を使う場合も解説します。

都立新宿高校2021年度　数学入試問題　4.場合の数と確率　問題

都立新宿高校2021年度　数学入試問題　4.場合の数と確率　問1解説解答

[問1]　点Bのy座標が、点Aのy座標より大きくなる確率を求めよ。

解説

a + b ＜ 2b　なので

a = 1のとき　b = 2，3，4，5，6

a = 2のとき　b = 3，4，5，6

a = 3のとき　b = 4，5，6

a = 4のとき　b = 5，6

a = 5のとき　b = 6

a = 1のとき　b なし

以上　15通り

または　下の表の通り

都立新宿高校受験プロ家庭教師

したがって　確率は

都立新宿高校2021年度　数学入試問題　4.場合の数と確率　問2　解説解答

問2 右の図2は、図1において直線ℓを一次関数 y = xのグラフとした場合を表している。点Aと点Bを結んだ場合を考える。直線ℓと線分ABが交わる確率を求めよ。ただし、点Aと点Bのどちらか一方が直線ℓ上にある場合も、直線ℓと線分ABが交わっているものとする。
高校受験プロ家庭教師東京

解説解答

点Aの座標(a，a + b)　点Bの座標(a，2b)　なので、点ABともにx座標は a，

よって直線ℓと線分ABが交わる場合は

ⅰ)　a + b ≦ a ≦ 2 b
　点Aのy座標より点Bのy座標が大きく2点間を　y = xが通るとき。a≩ 1　なので不能

ⅱ) 2b≦a≦a + b
　点Bのy座標より点Aのyざひょうが大きく2点間をy = xが通るとき
　a≦a + bは常に成立する。よって2b≦aとなる場合
(a，b)とすると、(2，1)(3，1)(4，1)(5，1)(6，1)(4，2)(5，2)(6，2)　以上9通り

または　下の表の通り

高校受験プロ家庭教師数学専門

したがって　確率は

都立新宿高校2021年度　数学入試問題　4.場合の数と確率　問3解説解答

問3　右の図3は、図1において、点Oと点A,点Oと点B，点Aと点Bをそれぞれ結んだ場合を表している。△OABの面積が3c㎡となる確率を求めよ。

プロ家庭教師都立高校受験

解説解答

点Aの座標(a，a + b)　点Bの座標(a，2b)　なので、高さを原点Oと点ABのx座標の差 aとした場合，底辺は点Aと点Bのy座標の差となる。

よって

ⅰ)　点Aのy座標より点Bのy座標が大きい場合
　　　a + b＞2b 　よって底辺の長さは　a + b - 2b = a - b
　　　したがって　△OABの面積が3c㎡となるのは　b ＜ a　かつ　a(a-b) = 6

ⅱ) 点Bのy座標より点Aのyざひょうが大きい場合
　　　a + b ＜2b　よって底辺の長さは　2b - (a + b) = b - a
　　　したがって　△OABの面積が3c㎡となるのは　a ＜ b　かつ　a(b - a) = 6

以上より　(a，b)とすると、(2，5)(3，5)(5，2)(5，3)　以上4通り

よって　確率は

有名進学塾、予備校カリキュラムに精通し、超難関中学受験、医学部受験、不登校、学力不振等、 多様な指導経験15年以上のプロ家庭教師たちが設立したプロ集団です。

都立新宿高校 過去問対策

東京都立新宿高等学校過去問研究

都立新宿高校2021年度 数学入試問題 4.場合の数と確率 問題

都立新宿高校2021年度 数学入試問題 4.場合の数と確率 問1解説解答