中学受験指導専門プロ家庭教師の学習院女子中等科過去問研究
学習院女子中等科受験指導はスペースＯＮＥのプロ家庭教師にお任せください。
 |
ご依頼専用ダイヤル |
0120-604-405 |
| お問い合わせ(東京本部) |
03-6868-6040 |
| お問い合わせ(福岡校) |
093-592-6658 |
 |
お問い合わせメール
|
|
 |
ws-spaceone |
|
プロ家庭教師集団スペースONE
中学受験案内HOME
インターネット指導コース
2013年度学習院女子中等科入試問題(過去問)解答解説
学習院女子中等科算数過去問研究
2013年度 算数Ａ入試問題は [1] 計算2問（四則計算，連比） [2] 場合の数 [3] 速さ [4] 平面図形（相似形応用） [5] 数列 ［6］ 平面図形の変形が出題されました。
今回は [4] 平面図形（相似形応用）を解説します。（１）の設問が（２）の解法のヒントになっています。題意をくみ取って解きましょう。
算数入試問題 平面図形にチャレンジ
問題[４]
プロ家庭教師集団スペースＯＮＥの解説・解答で学習院女子中等科の発表ではありません。
（１） 面積から高さを求める 解説解答
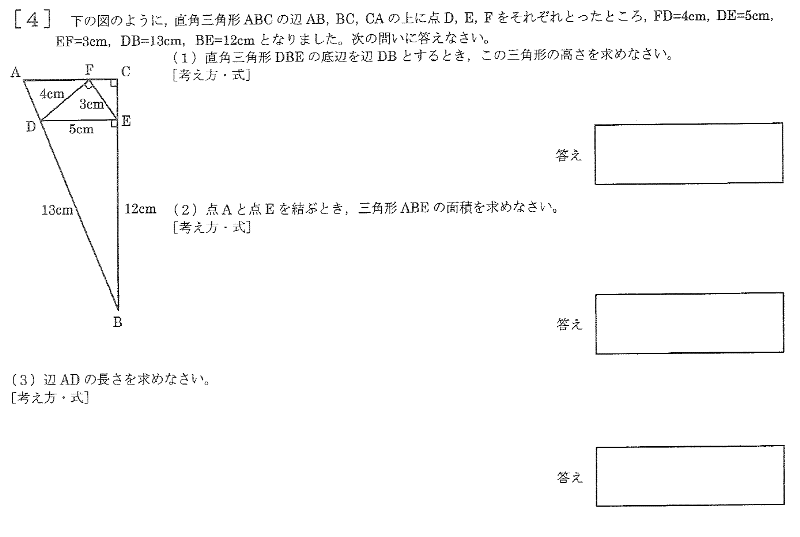
| (1) 直角三角形ＤＢＥの底辺を辺ＤＢとするとき、この三角形の高さを求めなさい。 |
|
| 解説 |
|
点Ｅから辺ＤＢに垂線をおろし、その交点をＥ’とする。直角三角形ＤＢＥの底辺を辺ＥＢとしたときの高さはＤＥなので
辺ＥＢ×辺ＤＥ＝辺ＤＢ×辺ＥＥ’
１２×５＝１３×辺ＥＥ’
辺ＥＥ’＝60/13 |
 |
| 答 60/13 cm |
|
|
|
（2） 解説解答
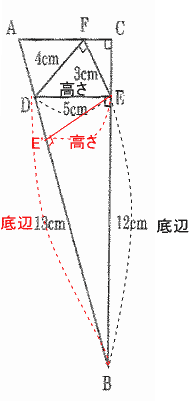
| (2) 点Ａと点Ｅを結ぶとき、三角形ＡＢＥの面積を求めなさい。 |
|
|
| 解説 |
|
|
|
| 三角形ＡＢＥの底辺をAＢとしたときの高さはＥＥ’。 |
 |
|
|
| よって ＡＢの長さを求めると良い。 |
|
|
| 三角形ＤＢＥと三角形ＡＢＣは相似形なので、辺ＢＥ：辺ＢＣの相似比＝辺ＢＤ：辺ＢＡの相似比 |
|
|
| 直角三角形ＦＤＥにおいて、点Ｆから辺ＤＥに垂線をおろしその交点をＦ’とすると、辺ＦＦ’＝辺ＣＥ |
|
|
| よって 辺ＣＥ＝辺ＦＦ’＝３×４÷５＝２．４（ｃｍ） |
|
|
| １２：１２＋２．４＝１３：辺ＢＡ 辺ＢＡ＝14.4×13÷12 |
|
|
| よって 三角形ＡＢＥの面積は （14.4×13÷12）×（12×5÷13）÷２＝14.4×5÷2＝３６ |
|
|
|
|
|
|
| 答 ３６ｃ㎡ |
|
|
|
|
|
（3） 解説解答
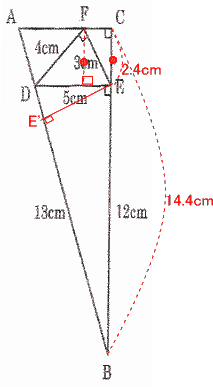
| (3) 辺ＡＤの長さを求めなさい。 |
|
|
| 解説 |
|
|
|
| 辺ＡＢー辺ＤＢ＝辺ＡＤ |
 |
|
|
| よって 14.4×13÷12ー13＝２．６ |
|
|
|
|
|
|
| 答 ２．６ｃｍ |
|
|
|
|
|
ＨＯＭＥ
このホームページのすべての文章の文責および著作権はプロ家庭教師集団スペース ONEに属します。
