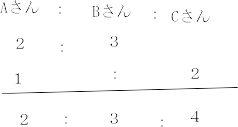中学受験はプロにお任せ/プロ家庭教師集団スペースONEの本郷中学校合格のための過去問対策2024年度算数入試問題小問集合解説解答

本郷中学校・高等学校過去問対策

中学受験指導はスペースONEのプロ家庭教師にお任せください。

本郷中学校合格のための過去問対策

2024年度本郷中学第1回入学試験は2月1日に実施され、募集人数100名に対し、応募者数516名　受験者461名　合格者164名　受験者最高点4科目267点　合格者最低点4科216点でした。

算数受験者最高点86点(昨年度比-8点)　受験者平均点54.2点(昨年度比-3.9点)　合格者平均点68.3点(昨年度比-3.8点)でした。

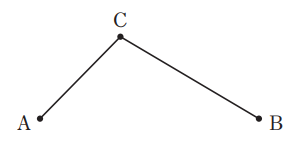
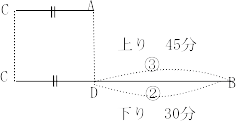
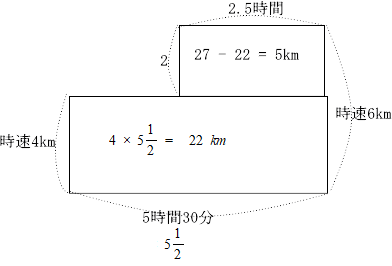
算数出題内容は1.四則計算2問　2.小問集合6問　3.速さ　4.規則性　5.立体図形の切断　が出題されました。

今回は　2.小問集合を解説します。5.速さ　6.立体図形の体積は、小問としては難問です。5.速さは聖光学院中学帰国生入試　6.立体図形の体積は　麻布中学の等積変形の類題です。

本郷中学受験指導はスペースONEのプロ家庭教師にお任せください。

本郷中学校2024年度算数入試問題2.小問集合　問題

本郷中学校2024年度算数入試問題2.小問集合　(1)仕事算解説解答

(1)　ある仕事をするとBさんはAさんの1.5倍、CさんはAさんの2倍の時間がかかります。3人いっしょにこの仕事をすると6時間かかります。Aさん１人だけでこの仕事をすると何時間かかりますか。

解説解答

BさんはAさんの1.5倍の時間がかかるので　AさんとBさんの時間の比は、1：1.5 = 2：3

CさんはAさんの2倍の時間がかかるので、AさんとCさんの時間の比は　1：2

連比より　AさんBさんCさんの時間の比は

よって　1時間当たりの仕事量の比は

3人いっしょにこの仕事をすると6時間かかるので　この仕事量は　(6 + 4 + 3)×6 = 78
Aさんが１人でこの仕事をするとかかる時間は

78 ÷ 6 = 13

答え　　　13時間

本郷中学校2024年度算数入試問題2.小問集合　(2)割合の文章題値段が一定解説解答

本郷中学校2024年度算数入試問題2.小問集合　(3)規則性解説解答

解説解答

1番目の分数の分子と分母の差は　2，2番目は　3,　3番目は 4,・・・・

よって　分子と分母の差が101になるのは　101 - 1 = 100番目の分数

分子は　1, 4, 7, 10・・・
初項は　1　交差は3　なので　100番目の分子の数は　1 + 3×(100 - 1) = 298

分母は　298 + 101 = 399

本郷中学校2024年度算数入試問題2.小問集合　(4)ニュートン算解説解答

(4)　ある製品を舞う分20個ずつの割合で作る工場があります。工場の中で作られた製品は、ベルトコンペアで工場の外へ運び出されます。いま、この工場の中には360個の製品が保管されています。ここで、さらに製品を作り始めたと同時に5台のベルトコンベアを使って運び出すと18分ですべての製品を工場の外へ運び出すことができます。このとき、製品を作り始めたと同時に7台のベルトコンベアを使って運び出すと何分ですべての製品を工場の外へ運び出すことができますか。

解説解答

5台のベルトコンベアが18分間で運び出す商品の数は　360 + 20×18

1台のベルトコンベアが1分間に運ぶ商品の数は　(360 + 20×18)÷(5×18) = 8個

よって　7台のベルトコンベアは保管していた360個の商品に加え1分間に20個ずつ作るのを7台のベルトコンベアが運び出すのにかかる時間は

360÷(7×8 - 20 ) = 10

答え　　　10分

本郷中学校2024年度算数入試問題2.小問集合　(5)解説解答

(5)　図のようにA地点からC地点までは上りで、C地点からB地点までは下りになっています。A地点からB地点に行くのに５時間30分、B地点からA地点に行くのに5時間45分かかります。このとき、BC間の距離は何kmですか。ただし、上るときは時速4km、下るときは時速6kmの速さで進むものとします。

解説解答

A地点からC地点まで上りでC地点からB地点に下って行くのに５時間30分、B地点からC地点まで上りでC地点からA地点に下って行くのに5時間45分かかるので、AC間の距離よりCB間の距離の方が長い。

CB間でAC間と等しい距離の地点をD地点とする。

DB間を上るのと下るのとで時間の差は　5時間45分 - 5時間30分 = 15分

上りの速さと下りの速さの比は　4：6 = 2：3

時間の比は　③：②　　よって　③ - ② = ① = 15分

DB間を下るのにかかる時間は　15×2 = 30分

したがって　A-C-D間の時間は　5時間30分 - 30分 = 5時間

AC = CD　なので　AC間を上るのにかかる時間とCD間を下るのにかかる時間の比は 3：2

よって　CD間を下るのにかかる時間は　2時間なので　CB間を下るのにかかる時間は　2時間30分

CB間の距離は　速さ　時速6kmで2時間30分かかるので

答え　　　15km

別解　速さの平均とつるかめ算で解く

解説解答

AB間の距離を１とし、A地点からB地点までを往復すると往復にかかる時間は

距離は2なので　往復の速さは

往復にかかった時間は5時間30分 + 5時間45分 = 11時間15分

よって　往復の距離は

AB間の距離は　54 ÷2 = 27km

AC間を時速4kmで上り、CB間を時速6kmで下ったので、つるかめ算の面積図より

CB間を下るのにかかった時間は　

時速6kmで2.5時間かかったので　CB間の距離は　6×2.5 = 15

答え　　　15km

本郷中学校2024年度算数入試問題2.小問集合　(6)解説解答

(6)　図1のような形を底面とする柱状の容器が図Ⅱのように水平な地面につくように置かれています。この容器に水を入れたら図Ⅲのようになりました。入れた水の体積は何c㎥ですか。ただし、容器の厚みは考えないものとし、円周率は3.14とします。

解説解答

図のように点O、A、B、C、D、Eをおく。

三角形OACと三角形OBEは　OA = OB = 8cm(おうぎ形の半径)　CO = BC = 4cm　角ACO = 角EO = 90°

OA：CO = OB：BC = 8：4 = 2：1　なので　角OAC = 角OBE = 30°

2辺とその間の角が等しいので　三角形OACと三角形OEは合同な三角形

三角形ODCが共通なので　三角形OADの面積 = 四角形DBECの面積

よって　扇形OABの面積 = ABDの面積 + 四角形DBECの面積

扇形OABの中心角 = 180° - (角OAC + 90°) - 角EOB = 180° - ( 30° + 90°) - 30° = 30°

したがって　斜線部分の面積 = 中心角30°　半径8cmのおうぎ形の面積 × 2