2009年度　開成中学校算数入試問題(過去問）解答解説

2009年度開成中学校の算数入試問題は　定番の平面図形、円高差益を題材にした今日的テーマの割合の文章題、煩雑な条件整理を必要とする数の性質・場合の数２題の大問４題構成でした。

算数入試問題　（平面図形の辺の比・面積比）

開成中学受験指導はスペースONEのプロ家庭教師にお任せください。

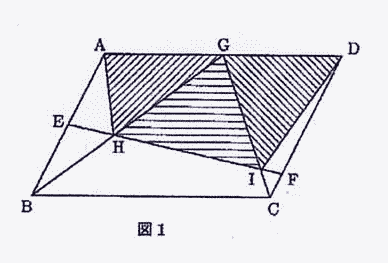
図１の四角形ＡＢＣＤは平行四辺形であり、点Ｅ，Ｆ，Ｇはそれぞれ辺ＡＢ，ＣＤ，ＤＡ上の点で、ＡＥ＝ＥＢ，ＡＧ＝ＧＤ，ＤＦ：ＦＣ＝４：１です。また、点ＨはＥＦとＢＧの、点ＩはＥＦとＣＧの交わる点です。　このとき、次の問に答えなさい。

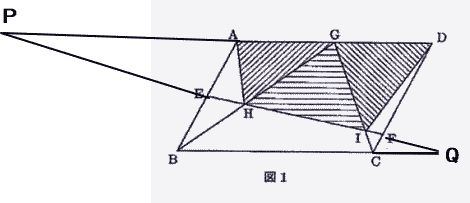
(1)　辺ＤＡを延長した直線と、ＦＥを延長した直線の交わる点をＰとします。また、辺ＢＣを延長した直線と、ＥＦを延長した直線の交わる点をＱとします。このとき、ＰＡ：ＡＤとＢＣ：ＣＱを求めなさい。

(2)　ＧＨ：ＨＢとＧＩ：ＩＣを求めなさい。

(3)　三角形ＡＨＧと三角形ＧＨＩと三角形ＧＩＤの面積の比を求めなさい。

(1) 辺ＤＡを延長した直線と、ＦＥを延長した直線の交わる点をＰとします。また、辺ＢＣを延長した直線と、ＥＦを延長した直線の交わる点をＱとします。このとき、ＰＡ：ＡＤとＢＣ：ＣＱを求めなさい。

解説解答

ＰＡ：ＢＱ＝ＡＥ：ＥＢ＝１：１　ＰＤ：ＣＱ＝ＤＦ：ＦＣ＝４：１　四角形ＡＢＣＤは平行四辺形なので　ＡＤ＝ＢＣ

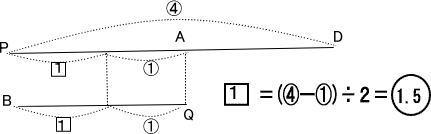ＰＡ：ＡＤ＝１．５＋１：１．５＝５：３　ＢＣ：ＣＱ＝１．５：１＝３：２

(2) ＧＨ：ＨＢとＧＩ：ＩＣを求めなさい。

解説解答

ＧＨ：ＨＢ＝ＰＧ：ＢＱ＝２.５＋（１.５÷２）：１.５＋１＝３.２５：２.５＝１３：１０

ＧＩ：ＩＣ＝ＰＧ：ＣＱ＝３.２５：１＝１３：４

(3)三角形ＡＨＧと三角形ＧＨＩと三角形ＧＩＤの面積の比を求めなさい。

解説解答

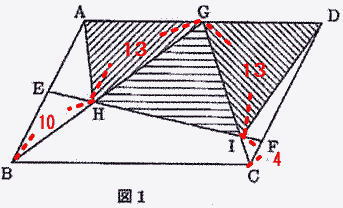四角形ABCDの面積を1にすると

答　　△AHG　：　△GHI　：　△GID　＝１７　：　２６　：２３

中学受験から医学部受験までプロ家庭教師にお任せください。