中学受験指導専門プロ家庭教師の芝中学校過去問研究
芝中学校受験指導はスペースＯＮＥのプロ家庭教師にお任せください。
 |
ご依頼専用ダイヤル |
0120-604-405 |
| お問い合わせ(東京本部) |
03-6868-6040 |
 |
お問い合わせメール
|
|
 |
ws-spaceone |
|
プロ家庭教師集団スペースONE
中学受験案内HOME
入会案内へ
芝中学校入試問題(過去問)解答解説
芝中学・高等学校2009年度算数過去問研究
2012年度芝中学校第１回算数入試問題は 例年通りの出題構成で １．計算２問 ２．〜１０． 一行問題・大問の組み合わせ。
出題内容は ２．数の性質 ３．割合の比（倍数変化算） ４．相当算 ５．立体図形の見取り図 ６．平面図形の面積比 ７．旅人算（速さのグラフ） ８．割合の文章題（食塩の濃度） ９．数の性質（倍数） １０．正三角形上の点移動 でした。
解答形式も例年通り 答のみを解答欄に書く形式でした。
2012年度第１回の算数合格者平均は63.7点 受験者平均は45.3点 例年より 受験者・合格者平均点が低く、難易度の高い出題内容でした。
芝中学校・高等学校受験 入試問題傾向と対策（過去問研究）ＴＯＰへ
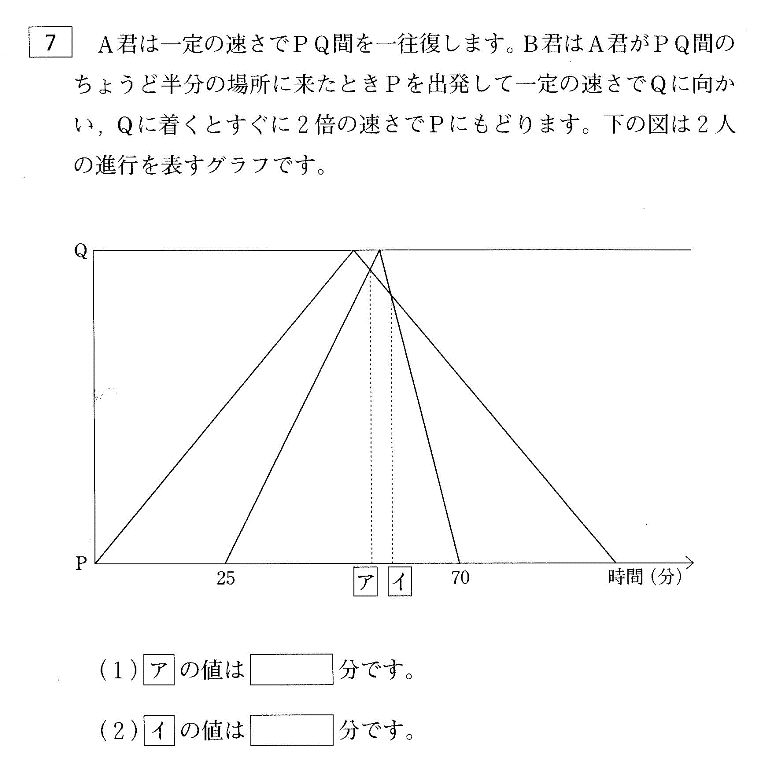
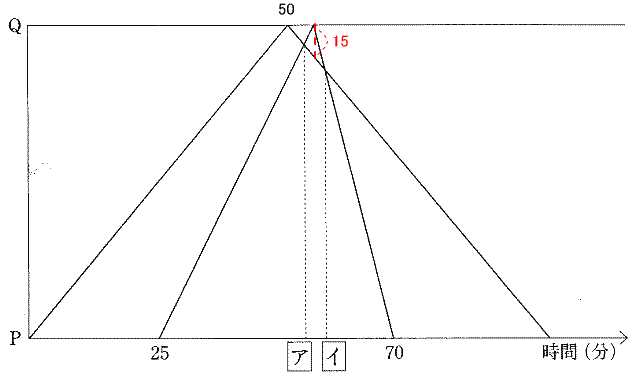
今回は7.速さのグラフを解説します。与えられた条件をグラフに書き込んで整理して解きましょう。
問題7
プロ家庭教師集団スペースＯＮＥの解説・解答で芝中学校の発表ではありません。
（１）速さの出会い算で解く解説解答
| ［ア］の値は［ ］分です。 |
| 解説 |
 |
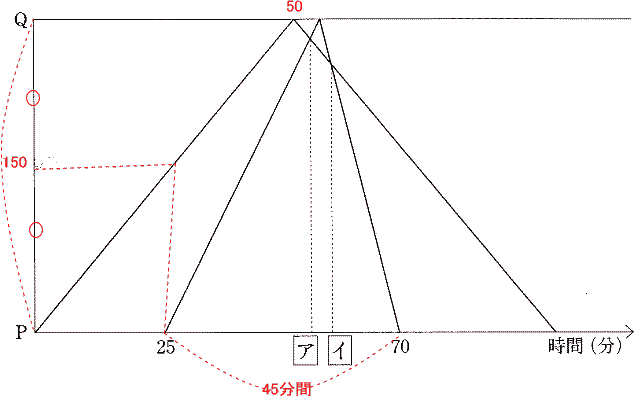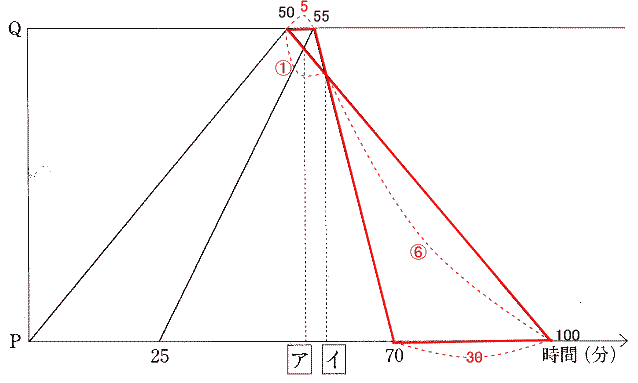
Ａ君は ２５分でＰＱ間の半分の場所に来ているので、Ａ君がＰＱ間を行くのにかかる時間は ５０分。
Ｂ君は ７０−２５＝４５分でＰＱ間を往復し、帰りは行きの２倍の速さなので、Ｂ君の往復の速さは １：２ よってかかった時間の比は ２：１
Ｂ君は行きに ４５÷３×２＝３０分 帰りに ４５÷３＝１５分かかっている。
Ａ君 Ｂ君の行き Ｂ君の帰りにかかる時間の比は ５０：３０：１５＝１０：６：３
よってそれぞれの速さの比は ３：５：１０
ＰＱ間の距離を ３×５０＝１５０とする。
|
 |
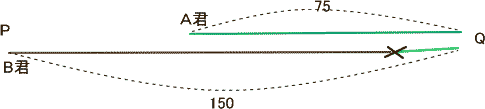| ［ア］の値はＡ君が出発して ２５分後から Ａ君とＢ君 二人で １５０＋７５＝２２５ 歩き出会った時間なので |
 |
|
|
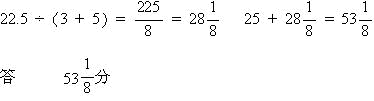（１）平面図形の辺の比で解く解説解答
| ［ア］の値は［ ］分です。 |
|
| 解説 |
|
（１）速さの出会い算で解く解説より
Ａ君がＰＱ間を行くのにかかる時間は ５０分。
Ｂ君は行きに ４５÷３×２＝３０分 かかる。
また Ａ君は往復に１００分かかるので、
右グラフの通り ５：７５＝１：１５
 |
 |
|
|
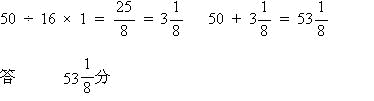（２）速さの追いかけ算で解く解説解答
| ［イ］の値は［ ］分です。 |
|
| 解説 |
|
Ｂ君がＱに着いたときのＡ君とＢ君の距離の差は、Ａ君が３の速さで５分間歩いた距離なので ３×５＝１５
この差をＢ君が１０の速さで追いかけるので
|
 |
|
|
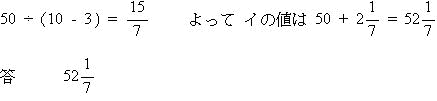
（２）平面図形の辺の比で解く解説解答
| ［イ］の値は［ ］分です。 |
| 解説 |
|
グラフの通り
(55 - 50)：(100 - 70) = 5：30 = 1：6
|
 |
|
|
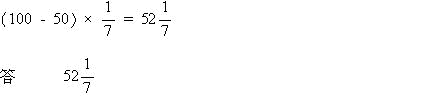
ＨＯＭＥ
このホームページのすべての文章の文責および著作権はプロ家庭教師集団スペース ONEに属します。
芝中学校過去問研究ＴＯＰに戻る