早稲田中学校・高等学校過去問対策
中学受験指導はスペースONEのプロ家庭教師にお任せください。
早稲田中学校合格のための過去問対策

早稲田中学校合格のための入試問題傾向と対策
過去問対策早稲田中学帰国生入学試験は一般受験生と同一日時に、同一問題で行います。また入学後は帰国生も一般生徒と同じクラスに受け入れ指導します。
2021年度早稲田中学算数入試問題は例年通り大問5題構成で、(1)小問集合3問,(2)平面図形3問,(3)場合の数,(4)立体上の点移動のグラフ,(5)平面図形上の点移動が出題されました。(5)の作図問題以外解答の身を課k当欄に書く解答形式でした。
今回は (4)立体上の点移動を詳しく解説します。
(1) 四角形の面積をもとに、縦の長さと横の長さの比からそれぞれの長さを求める場合、直感的には、横に4本、縦に5本の線を引いて30個の正方形ができるので1つの正方形の面積が4㎠になることから小さい正方形の一辺が2cmだと考えるのがわかりやすいです。
(2)は三角形の斜辺の長さが変化することに気づかないと間違えてしまいます。
速さが途中から変わります。よって辺の長さも変化することに気をつけましょう。
早稲田中学校2021年度算数入試問題 4.立体上の点移動 問題
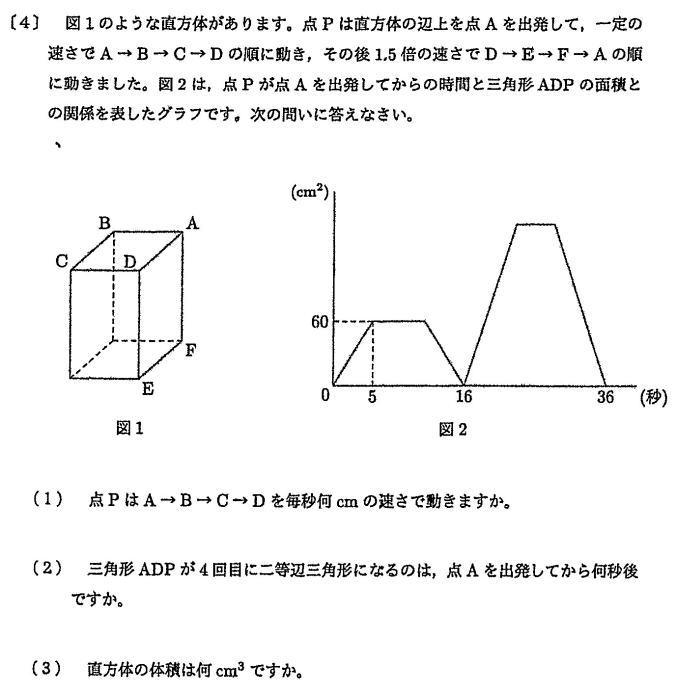
早稲田中学校2021年度算数入試問題 4.立体上の点移動 (2) 解説解答
(2) 三角形ACPが4回目に二等辺三角形になるのは、点Pを出発して何秒後ですか。
解説解答
点PがAB上,CD上を動くとき
三角形ADPは直角三角形になる。よって二等辺三角形になる場合は直角二等辺三角形となる。したがって AB < DAとなるので、辺AB,辺CD上では二等辺三角形となることはない。
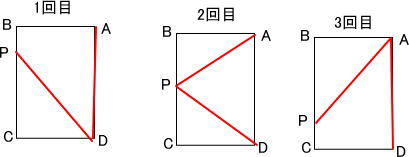
辺BC上を点Pが動くとき、
AP = DAに点PがB上にあるときBDは直角三角形ABDの斜辺なのでAB<AD<BD。 BD>12cm,
点PがBCの中点にあるとき AP = PDの二等辺三角形の辺APは直角三角形ABPの斜辺でAB:BP = 10:6 = 5:3なので AP = 8cm,
よって 点PがBC上を動くときPDの長さは8cmから12cm以上の長さになっていくので、AD = PD,AP = PD,AP =
ADと二等辺三角形になる場合が3回ある。
4回目
D→E→R→Aを点Pは 2×1.5 = 3cm/秒で、36 - 16 = 20秒間で動くので動いた長さは 3×20 = 60cm
EF = DA = 12cm なので、DE = AF = (60 - 12)÷2 = 24cm
したがって、4回目はAD = DP = 12cmになるとき。
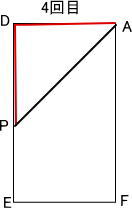
よって、16 + 12÷3 = 20
答 20秒後