第2回 消去算を例に挙げて中学受験の特殊算を学習しましょう。
例1消去算 3・4年生基本問題 一方がそろっている問題
問題1 りんごが2個とみかん5個で550円、りんご4個とみかん5個で750円のとき、りんご、みかんはそれぞれいくらですか。
具体物を用いて理解したうえで、線分図で置き換えてみましょう。
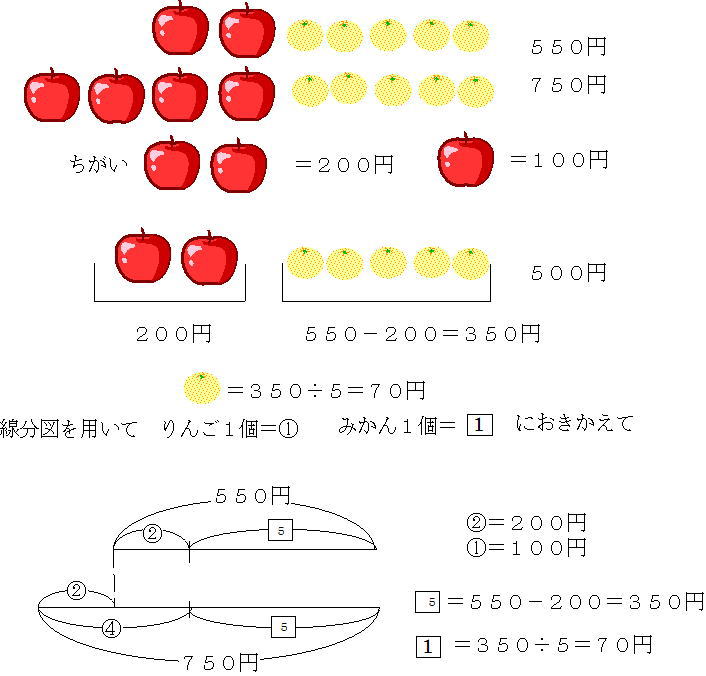
具体物から線分図への置き換えは、五年生からの学習に必須です。何度も繰り返して慣れましょう。特に一方がすでにそろっている問題は、倍数変化算の「和が一定問題」へとつながっていきます。問題文に沿って適切な線分図が書けるようになりましょう。
第3回例2 倍数変化の考え方を用いて
一方の数をそろえる問題。
りんご2個とみかん3個で410円、りんご3個とみかん5個で650円のとき、りんごとみかんの値段はそれぞれいくらですか。
まず、表に整理して考えていきましょう。
| りんごの個数 |
みかんの個数 |
金額 |
| 2 |
3 |
410円 |
| 3 |
5 |
650円 |
りんごの個数とみかんの個数がそれぞれ違うので、どちらかに個数を合わせます。
ここでは、りんごの個数にあわせましょう。2と3の小公倍数6にするためそれぞれを3倍2倍にすると
| |
りんごの個数 |
みかんの個数 |
金額 |
| |
6 |
9 |
1230円 |
| |
6 |
10 |
1300円 |
| 違い |
|
1 |
70円 |
表より みかん1個=70円
よって、りんご1個・・・410-(70×3)÷2=100円
この一方のそろえる問題も、線分図を用いて計算するとどうなるでしょう。次回はこの問題を線分図で解きましょう。
第4回 例2 線分図で解きましょう。
りんご1個を①,みかん1個を[1]におきます。
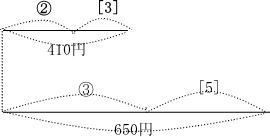
表と同様りんごに数を合わせて線分図を描きましょう
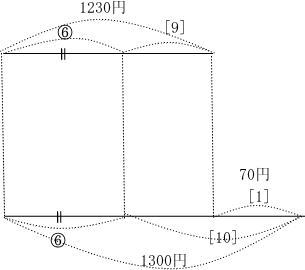
線分図に表すと線の長さがそのもの違いとして理解がしやすいようです。
線分図の描き方によく慣れて問題文をそのまま線で表現できるようになりましょう。
第5回 例3 2つの差に注目する問題。
イチゴ2個と、みかん3個では、900円、イチゴ3個と、みかん2個で850円です。
イチゴとみかんの値段は、それぞれいくらですか。
表にして考えましょう。
| |
 |
 |
金額 |
| |
2 |
3 |
900円 |
| |
3 |
2 |
850円 |
| 違い |
1 |
1 |
50円 |
表より、イチゴ1個とみかん1個の値段の差は50円で、みかん1個はイチゴ1個より50円高い。
よって、みかんをイチゴに置き換えると
イチゴ5個・・・900-50×3=750円
イチゴ1個・・・750÷5=150円
みかん1個・・・150+50=200円
第6回 例4 2つの差に注目する問題。(豊島岡学園女子中学校入試問題)
例4 本を2冊とノートを5冊買うと代金は1280円です。また本1冊とノート4冊の合計代金と本2冊とノート3冊の合計代金の差は220円です。このとき本1冊の値段はいくらですか。
難関校の問題ですが、例3と同様、表にして考えると
| |
本 |
ノート |
値段 |
| |
1 |
4 |
|
| |
2 |
3 |
|
| 違い |
1 |
1 |
220円 |
例3と違い、本とノートのどちらが高いかがわからないので、①本が高い場合、②ノートが高い場合に分けて考えます。
① 本2冊 ノート5冊 1280円
本2冊=ノ-ト2冊+220×2=440円
ノート7冊=1280-440=840
よってノート1冊・・・840÷7=120円
②も同様に計算すると(以下省略)、割り切れなくなるので、答えは、①の場合になります。
この問題は、本が高いかノートが高いかの条件を加えるだけで、例3と難易度の差はほとんどありません。
 第7回 例5 倍数と置き換えの問題
第7回 例5 倍数と置き換えの問題
ショートケーキ1個の値段は、プリン1個の値段の3倍で、ショートケーキ4個とプリン6個を買ったら1,800円でした.。プリン1個の値段はいくらですか。
ショートケーキをプリンに置き換えましょう。
表より プリン18個で1,800円。
プリン1個では 100円
第8回 倍数と置き換えの問題例6(女子聖学院3回類題)
雑誌2冊の値段とボールペン7本の値段が同じとき、雑誌10冊とボールペン8本を買うと1290円です。このとき雑誌1冊の値段はいくらですか。
例5度同様、図示して考えるほか、計算式にすると、
ボールペン 7×5+8=43本 で1290円なので、
ボールペン1本・・・1290÷43=30円
雑誌 ・・・30×7÷2=105円
別解
雑誌1冊とボールペン1本の値段の比
ザ×2=ボ×7=1
7 : 2
よって 7×10+2×8=86
86・・・1289円に相当する
雑誌1冊・・・1290÷86×7=105円
このような一行問題では、一問あたりにかけられる時間は2~3分の場合が多いので、スピードと正確さという点から見ると、比を使いこなす必要性をここで見て取れるでしょう。
以上のように、例1・2・3・5は、四年生の塾教材に含まれている問題ですが、例4・6では、教科書としては6年生の範囲に入る倍数を4年生ですでに学んでいることを前提としており、また、入試レベルの問題を四年生の学習内容に入れている場合が多い。難関校の入試レベルの問題をも含む塾教材中のすべての問題をこなす事だけに力点が入ると、問題の内容を理解せず丸暗記型の学習になり応用力が身につかなくなる可能性が高い。四年生では、りんご・みかんなどの絵から、線分図で問題文を表現できるまでの基礎的な準備を十分にしておきさえすれば、五年生での基礎からの復習を応用倍数変化算、比の応用問題につなげられると考えられます。
視覚的に十分納得させた後、通分することの意味を確認し、紙上のみの学習へと移ることが望ましい。また、分数の計算で必須な約数・倍数も、塾教材では一足飛びに素因数分解を用いるが、六年の教科書にある2つの数・3つの数それぞれの倍数・約数を出して、共通する約数・倍数を求める方法を繰り返し、その意味を十分納得した後、塾教材へと段階的に理解を伸ばしていくと、5年の2学期に学習する「比」では、逆数の理解や、比の簡略化の処理が円滑にでき、比を取り違えるなどの苦労を未然に防ぐことになろう。
平面図形、立体図形、点・線・対称図形を5年生の学習で理解しやすいように、画用紙・工作用紙・グラフ用紙を用いて、三角定規・コンパス・分度器を使いこなす練習を繰り返してほしい。円に内接する正多角形・三角形・四角形(台形・平行四辺形・ひし形など)・おうぎ形の作図、平面図(展開図)の組み立てによる表面積、体積、さらには複数の立体図形の重なり方を三方向(六方向)から、どのように見えるかを確認し、さらに粘土(頂点)と竹ひご(辺)で立体を作り、3点、4点で立体図形を分割したときにできる平面の形の確認や、頂点、辺を増やすときの図形の数の規則的な増え方まで、視覚的に、そして皮膚感覚として実体験してほしいものである。平面図形の面積や、角度の出し方、立体図形の展開図や、図形の分割など、図形の中に隠されている条件を読み取る練習を家庭学習として、十分時間の取れる時期につんでいてほしい。空間感覚、平衡感覚を要求される学習は、一朝一夕に身につくものではないだろう。
第9回 計算・平面図形への対応
つぎに、計算に関しては、五年六年の教科書の学習範囲にある分数、小数の四則計算も、塾教材では四年の学習範囲です。この分数、小数の概念も、具体物から抽象化への一助として、パン、チョコレート、ケーキなど、大きさ、形の異なるものを分割し、視覚的に十分納得させた後、通分することの意味を確認し、紙上のみの学習へと移ると分数への抵抗感が少なくすむようです。また、分数の計算で必須な約数・倍数も、塾教材では一足飛びに素因数分解を用いますが、六年の教科書にある2つの数・3つの数それぞれの倍数・約数を出して、共通する約数・倍数を求める方法を繰り返し、その意味を十分納得した後、塾教材へと段階的に理解を伸ばしていくと、5年の2学期に学習する「比」では、逆数の理解や、比の簡略化の処理が円滑にでき、比を取り違えるなどの苦労を未然に防ぐことになるでしょう。
平面図形、立体図形、点・線・対称図形を5年生の学習で理解しやすいように、画用紙・工作用紙・グラフ用紙を用いて、三角定規・コンパス・分度器を使いこなす練習を繰り返してほしい。円に内接する正多角形・三角形・四角形(台形・平行四辺形・ひし形など)・おうぎ形の作図、平面図(展開図)の組み立てによる表面積、体積、さらには複数の立体図形の重なり方を三方向(六方向)から、どのように見えるかを確認し、さらに粘土(頂点)と竹ひご(辺)で立体を作り、3点、4点で立体図形を分割したときにできる平面の形の確認や、頂点、辺を増やすときの図形の数の規則的な増え方まで、視覚的に、そして皮膚感覚として実体験してほしいものです。平面図形の面積や、角度の出し方、立体図形の展開図や、図形の分割など、図形の中に隠されている条件を読み取る練習を家庭学習として、十分時間の取れる時期につんでいてほしい。空間感覚、平衡感覚を要求される学習は、一朝一夕に身につくものではないからです。
参考入試問題

 四年生の社会の学習法
四年生の社会の学習法  四年生の理科の学習法
四年生の理科の学習法  四年生の国語の学習法
四年生の国語の学習法

 INDEX
INDEX




 第7回 例5 倍数と置き換えの問題
第7回 例5 倍数と置き換えの問題
