(3) 点Pが途中8個以下の交点を通って、点Bに到着する移動方法は全部で何通りありますか。
解説解答
3個の交点を通過する場合も含めて
1+4+10+20+35+56=126
答126通り
プロ家庭教師集団 スペースONE聖光学院中学帰国生受験 入試問題 Eラーニング (過去問対策)
2022年度聖光学院中学帰国生入学試験は 2022年1月9日に実施されました。入試結果は、 募集人数 若干名,応募者数153名(前年比-12名) 受験者数144名(前年比-18名) 合格者35名(前年比-4名)でした。
国語 配点100点 合格者最高点86点 合格者最低点48点 合格者平均点68.0点 受験者平均点57.2点でした。
算数 配点100点 合格者最高点100点 合格者最低点59点(前年比 +20点) 合格者平均点78.9点(前年比 +12.3点) 受験者平均点58.5点(前年比 + 17.9点)でした。
英語 配点100点 合格者最高点71点 合格者最低点51点 合格者平均点61.9点 受験者平均点48.7点でした。
国語算数合格者最高点 178点 合格最低点137点(前年比 + 10点) 合格者平均点152.7点 受験者平均点 119点,英語算数合格最高点 165点 合格最低点 120点(前年比 + 34点) 合格者平均点 133.1点 受験者平均点 101.2点でした。
2022年度聖光学院中学帰国生算数入試問題は、昨年度まで大問1題が速さの問題でしたが、今年度は1.小問集合に入り、(1)四則計算 (2)速さ (3)過不足算 2.食塩水の文章題 3.場合の数 4.立体図形 5.平面図形が出題されました。
昨年度より合格者最低点が 20点あがったのは、大問速さが 図形を中心とした出題構成に変わったことによるものと考えられます。
今回は 3.場合の数を解説します。小学生ならどう考えるのか?小学生が理解できるように解説しています。

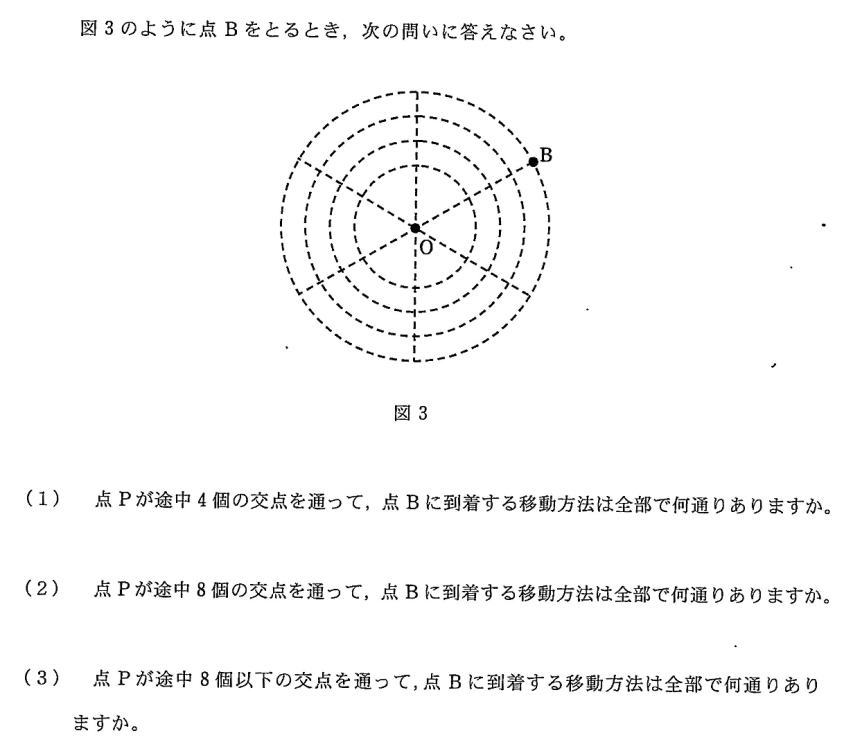
(1) 点Pが途中4個の交点を通って、点Bに到着する移動方法は全部で何通りありますか。
解説解答
点Pは、半径上の移動と円周上の移動 があります。
円周は半径で区切られた弧を内側から①、②、③、④とします。
半径OB以外の半径を図のようにア、イ、ウ、エ、オとします
半径はそれぞれ円で四分割されてます。四分割された線はどれかの半径で一回しか通れません。
たとえば下の図でOからBに直線上をまっすぐ進むとき4つの線移動となります。。
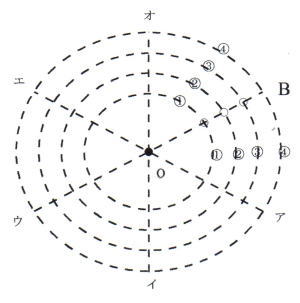
点Pが中心Oから点Bに移動するとき交点の最も少ない場合は、中心Oから点Bまで半径上のみを進む場合で通過する交点の数は3個です。
4個の交点を通って点Bにつく場合は、中心Oから半径アの方向に進む場合のみです。
アからBへ①を通る場合1通り、②を通る場合1通り、③を通る場合1通り、④を通る場合1通り、合計4通りです。
答 4通り
(2) 点Pが途中8個の交点を通って、点Bに到着する移動方法は全部で何通りありますか。
解説解答
5個の点を通って点Bにつく場合は、中心Oから半径イの方向に進む場合のみです。
半径イから半径アへ①を通っていく場合は、半径アと弧①の交点からは、半径アから半径Bへの①から④のすべての弧の上を通る場合がある。
よって①を通るXはX=1+1+1+1=4通りとなる。
半径イから半径アへ②を通っていく場合は、半径アと弧②の交点からは、半径アから半径Bへの②から④のすべての弧の上を通る場合がある。
よって②を通るYはY=1+1+1=3通り
同様にしてZ=1+1=2通り、W=1通り
これらを足して10通り
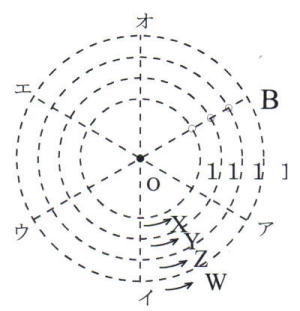
5個の交点を通る場合 10通り
6個の交点を通って点Bにつく場合は、中心Oから半径ウの方向に進む場合
7個の交点を通って点Bにつく場合は、中心Oから半径エの方向に進む場合
8個の交点を通って点Bにつく場合は、中心Oから半径オの方向に進む場合
これらから各弧を通って進む数を記入すると下の図のようになる。
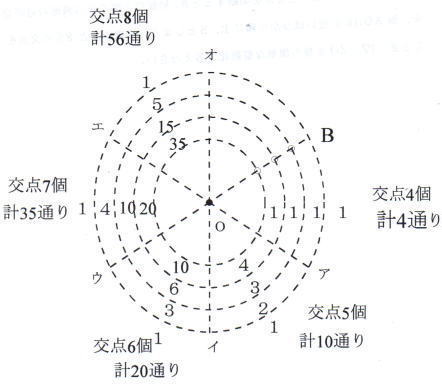
答56通り
国語 配点100点 合格者最高点86点 合格者最低点48点 合格者平均点68.0点 受験者平均点57.2点でした。
算数 配点100点 合格者最高点100点 合格者最低点59点(前年比 +20点) 合格者平均点78.9点(前年比 +12.3点) 受験者平均点58.5点(前年比 + 17.9点)でした。
英語 配点100点 合格者最高点71点 合格者最低点51点 合格者平均点61.9点 受験者平均点48.7点でした。
国語算数合格者最高点 178点 合格最低点137点(前年比 + 10点) 合格者平均点152.7点 受験者平均点 119点,英語算数合格最高点 165点 合格最低点 120点(前年比 + 34点) 合格者平均点 133.1点 受験者平均点 101.2点でした。
2022年度聖光学院中学帰国生算数入試問題は、昨年度まで大問1題が速さの問題でしたが、今年度は1.小問集合に入り、(1)四則計算 (2)速さ (3)過不足算 2.食塩水の文章題 3.場合の数 4.立体図形 5.平面図形が出題されました。
昨年度より合格者最低点が 20点あがったのは、大問速さが 図形を中心とした出題構成に変わったことによるものと考えられます。
今回は 3.場合の数を解説します。小学生ならどう考えるのか?小学生が理解できるように解説しています。
| 聖光学院中学2021年度帰国生算数入試問題3.場合の数 問題 |


| 聖光学院中学2021年度帰国生算数入試問題3.場合の数(1)解説解答 |
(1) 点Pが途中4個の交点を通って、点Bに到着する移動方法は全部で何通りありますか。
解説解答
点Pは、半径上の移動と円周上の移動 があります。
円周は半径で区切られた弧を内側から①、②、③、④とします。
半径OB以外の半径を図のようにア、イ、ウ、エ、オとします
半径はそれぞれ円で四分割されてます。四分割された線はどれかの半径で一回しか通れません。
たとえば下の図でOからBに直線上をまっすぐ進むとき4つの線移動となります。。

点Pが中心Oから点Bに移動するとき交点の最も少ない場合は、中心Oから点Bまで半径上のみを進む場合で通過する交点の数は3個です。
4個の交点を通って点Bにつく場合は、中心Oから半径アの方向に進む場合のみです。
アからBへ①を通る場合1通り、②を通る場合1通り、③を通る場合1通り、④を通る場合1通り、合計4通りです。
答 4通り
| 聖光学院中学2021年度帰国生算数入試問題3.場合の数 (2)解説解答 |
(2) 点Pが途中8個の交点を通って、点Bに到着する移動方法は全部で何通りありますか。
解説解答
5個の点を通って点Bにつく場合は、中心Oから半径イの方向に進む場合のみです。
半径イから半径アへ①を通っていく場合は、半径アと弧①の交点からは、半径アから半径Bへの①から④のすべての弧の上を通る場合がある。
よって①を通るXはX=1+1+1+1=4通りとなる。
半径イから半径アへ②を通っていく場合は、半径アと弧②の交点からは、半径アから半径Bへの②から④のすべての弧の上を通る場合がある。
よって②を通るYはY=1+1+1=3通り
同様にしてZ=1+1=2通り、W=1通り
これらを足して10通り

5個の交点を通る場合 10通り
6個の交点を通って点Bにつく場合は、中心Oから半径ウの方向に進む場合
7個の交点を通って点Bにつく場合は、中心Oから半径エの方向に進む場合
8個の交点を通って点Bにつく場合は、中心Oから半径オの方向に進む場合
これらから各弧を通って進む数を記入すると下の図のようになる。

答56通り
| 聖光学院中学2021年度帰国生算数入試問題3.場合の数 (3)解説解答 |
 |
聖光学院中学校帰国生入試問題(スペースONEプロ家庭教師算数・国語模範解答)を頒布中です。(1年度1科目1,500円) 2023年度・2024年度・2025年度解説解答はオンライン指導で承っております。 |
| 頒布 模範解答: 算数:2022年度・2021年度・2020年度・2019年度・2018年度・2017年度・2016年度・2015年度・2014年度・2013年度・2012年度・2011年度 国語:2022年度・2021年度・2020年度・2019年度・2018年度・2017年度・2016年度・2015年度・2014年度・2013年度・2012年度・2011年度 英語:2016年度・2011年度 |
|
 |
メールでお問い合わせください。pro.tutor@ws-spaceone.jp 着信拒否設定がなされスペースONEからの返信メールが送れない場合がございます。弊社からの返信メールがない場合(03-4363-5472または090-3432-2593),skype(ws-spaceone)にお問い合わせください。 |
